Определение месторасположения склада

Для решения одной из фундаментальных логистических задач-определения месторасположения распределительного склада в регионе необходимо знать:

¾    месторасположение (координаты xi, yi)  фирм-производителей и потребителей (клиентов) данной продукции;

¾    объемы поставок продукции (Qi);

¾    маршруты доставки (характеристику транспортной сети);

¾    затраты (или тарифы) на транспортные услуги (Ti).

В зависимости от выбранного критерия оптимизации и учета расстояний между поставщиками, потребителями и складом рассматриваются следующие типовые случаи.

Первый вариант. Месторасположение распределительного склада определяется в виде координат центра тяжести грузовых потоков по формулам:

,                                       (14.1)

,                                       (14.2)

где:  Ax,  Ay – координаты распределительного склада, км;

Qi – объем (вес) груза, т;

xi yi – соответственно расстояние от начала осей координат до расположения поставщика или клиента, км.

Второй вариант. Месторасположение склада определяется как «центр равновесной системы транспортных затрат». Расчет координат склада производится по формулам:

,                                 ( 14.3)

,                                 (14.4)

где Ti – транспортный тариф для i – го поставщика или потребителя (клиента), руб.т. км.

Суммирование в формулах (14.1) – (14.4) производится от i=1 до m, где m – общее количество поставщиков и потребителей.

Очевидно, что при Ti =const., формулы (14.1), (14.2) и (14.3), (14.4) совпадают.

С другой стороны, транспортные тарифы Ti в формуле (14.3), (14.4) играют роль весовых коэффициентов, которые могут принимать различные значения и, следовательно, расширяют возможности учета различных факторов по сравнению с формулами (14.1), (14.2). Тарифы функционально связаны с грузооборотом (т. км) и объемом перевозок (т), поэтому их упрощенный учет в расчетных зависимостях требует дополнительного обоснования, либо введения более сложных зависимостей.

Рассмотрим пример расчета координат склада по первому и второму вариантам. Исходные данные о координатах расположения поставщиков Пi и клиентов Кi приведены в табл. 14.1; также представлены вспомогательные расчеты. При подстановке значений в формулы (14.1),( 14.2) находим

Аx =  км,

  Ay =  км.

Второй вариант расчета, формулы (26.3), (26.4) дает:

Аx =  км,

Ay = км.

Приведенные на рисунке 14.1 местоположение складов показывают, что в данном конкретном случае их координаты различаются незначительно.

Таблица 14.1

Определение координат склада

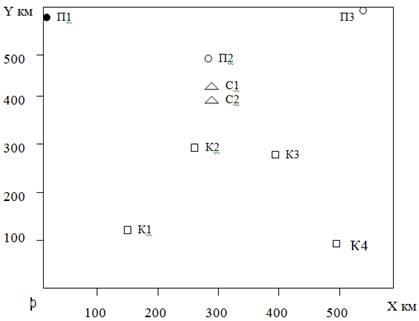
Рисунок 14.1 Расположение поставщиков П, клиентов К и складов: С1 – первый вариант; С2 – второй вариант.

Третий вариант. Координаты склада определяются исходя из условия, что сумма расстояний от данных точек m с учетом спроса Qi  до точки (x,y) – координат склада – была минимальной. Целевая функция записывается в виде:

        (14.5)

где ai, bi – координаты i-го поставщика или потребителя.

Принципиальное отличие третьего варианта заключается в том, что, во-первых, он сформулирован как классическая оптимизационная задача, во-вторых, расстояние между складом и другими объектами определяется как «гипотенуза», тогда как в задачах первом и втором вариантах рассматриваются расстояния по осям X и Y.

Для нахождения координат склада используется аналитический метод, согласно которому на первом  этапе определяется система из 2-х уравнений в виде частных производных функций P (x,y).

;                       (14.6)

Поскольку решение данной системы затруднено, на втором этапе используется итерационный метод. Так первое приближение для x(1) рассчитывается по формуле:

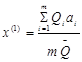                                                   (14.7)

Входящее в формулу  определяется из уравнения

                                  (14.8)

На третьем этапе значения x(1) подставляется во второе уравнение системы (14.6) для частной производной по Y и находится первое приближение для y(1). Затем y(1) подставляется в уравнение для частной производной по X и находится второе приближение x(2) и т.д. до тех пор, пока разница итераций P(k) (x,y) и P(k+1) (x,y) не станет меньше достаточно малого положительного числа E.

Однако, попытка использовать описанный итерационный метод решения наталкивается на такие же трудности, как и аналитическое решение системы (14.6).

Это нетрудно показать на следующем примере. Запишем в явном в виде первое уравнение системы (14.9).

                                (14.9)

Допустим, что m=2, a x(1) рассчитано по формуле (26.7) тогда, для нахождения y(1) надо решить уравнение:

          (14.10)

После преобразований получим кубическое уравнение для определения y(1): очевидно, что с увеличением m расчетные формулы усложняются, следовательно, использование итерационного подхода не упрощает поиск координат склада.

Рассмотрим подход, основанный на непосредственном поиске минимума функции (14.5). Исходные данные для расчетов приведена в таблице 14.1.

Для примера рассчитаем величину транспортной работы при перевозках от производителей на склад и со склада клиентам, выбрав в качестве координат склада следующие значения:

x1=250 км, y1 = 425 км. Тогда по формуле (14.5) для первого поставщика (а1 = 300 км, b1 = 575 км) находим:

т.км.

Результаты расчетов Р(x1, y1) для всех поставщиков и клиентов приведены в табл. 14.2: Р(x1, y1)≈342 тыс.км

Таблица 14.2

Определение транспортной работы при координатах склада х1 = 250 км, у1 = 425 км

Анализ результатов позволил выявить направление поиска координат склада (второй блок, три точки), изменив его вдоль координаты х = 300 км. Наконец, минимальное значение транспортной работы оказалось равным Р = 329950 т.км. (при принятом в расчетах шаге ∆ = 25 км), что соответствует координатам склада: х = 300 км; у = 500 км.

Таблица 14.3

Определение координат склада (численный метод)

Следует подчеркнуть, что разница значений Р (х, у) между 6 и 7 вариантами составляет 0,46%, а между 9 и 7 – 0,1%. С одной стороны это затрудняет поиск минимума функции Р(х, у), с другой стороны говорит о том, что минимум Р(х, у) при заданном выражении целевой функции соответствует область значений, незначительно отличающихся друг от друга. Таким образом, с небольшой погрешностью координаты склада могут быть выбраны внутри этой области, что позволяет учесть всевозможные и часто противоречивые ограничения: административные, правовые и т.п.