Устранение источников погрешностей до начала измерений (профилактика погрешностей)
Способ устранения предполагаемых погрешностей до начала измерений является наиболее рациональным, так как полностью или частично освобождает от необходимости устранять погрешности в процессе измерения или вычислять результат с учетом поправок.
Перед измерением объект измерения должен быть изучен для корректного выбора его модели и средств измерений, проанализированы возможные источники систематических погрешностей для снижения влияния дополнительных погрешностей на результат измерения, приняты возможные меры для устранения влияния источников погрешностей.
Под устранением источника погрешности понимается защита измерительной аппаратуры и объекта измерения от влияния источника погрешности либо удаление этого источника.
Удалить источники значительных инструментальных погрешностей возможно при ремонте и регулировке, необходимость проведения которых выявляется при очередных и внеочередных поверках средств измерений.
Систематические погрешности от неправильной установки могут быть значительно снижены при подготовке места установки средства измерения.
Для устранения влияния температурной погрешности широко используются термостатирование, т.е. обеспечение стабильной (в определенном интервале) температуры окружающей среды, кондиционирование и т.д.
Для устранения погрешностей от влияния магнитных и электрических полей применяется экранирование из магнитомягких материалов или материалов с высокой электропроводностью. Для устранения влияния равномерных магнитных полей используются астатированные средства измерений.
Уменьшение погрешностей от воздействия тряски и вибраций достигается установкой приборов на массивные подставки, а также использованием различных поглотителей колебаний - струнных и пружинных амортизаторов, губчатой резины и т.п.
Уменьшить влияние погрешностей от воздействия давления и влажности окружающей среды можно, используя барокамеры различных конструкций.
Следует принять меры для уменьшения влияния средств измерений на измеряемый объект, в результате которого могут произойти изменения режимов работы цепи при включении в нее средства измерения. Для этого выполняются различного типа согласования.
2. Исключение погрешностей в процессе измерения
Исключение погрешностей в процессе измерения - экспериментальное исключение погрешностей. При этом не применяются какие-либо специальные установки и приспособления. Как правило, это методы и приемы измерений, позволяющие исключить или существенно снизить систематические погрешности измерений. Следует отметить, что исключению погрешностей в процессе измерений поддаются, в основном, инструментальные погрешности, погрешности установки и погрешности, вызванные влиянием внешних условий.
Используются методы замещения, компенсации погрешности по знаку, противопоставления, симметричных наблюдений. Характерным признаком используемых методов является необходимость проведения повторных измерений, поэтому они применимы, в основном, при определении стабильных погрешностей либо погрешностей, изменяющихся по известным законам.
Метод замещения является разновидностью метода сравнения с мерой. Суть этого метода состоит в замене измеряемой величины величиной, известной с большой точностью. Причем последняя должна находиться в тех же условиях, что и измеряемая физическая величина. Если в результате замены не происходит изменений режимов работы, то делается вывод, что измеряемая величина равна значению меры. Это позволяет исключить остаточную погрешность мостовых цепей, ошибки градуировки шкал и т.д.
Пример – измерение сопротивления резистора с заменой его магазином сопротивлений и подбором сопротивления магазина такой величины, чтобы ток через резистор и магазин сопротивлений были равны.
 |
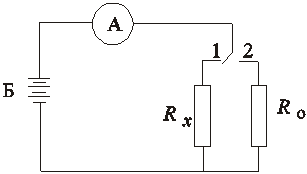Так, согласно рис. 3.2, измерения проводятся вначале в первом положении ключа. В этом положении регистрируется ток I1 через измеряемое сопротивление Rx, затем ключ переводится в положение 2 и магазин сопротивлений Ro подбирается такой величины, чтобы ток в этом
Рис. 5.2. Измерение сопротивления методом замещения
положении был равен току I1. Если I1 = I2, значит, и Rx = Ro. Получаемый результат измерения обладает точностью, близкой к точности магазина сопротивлений, так как погрешность измерения амперметра практически не влияет на точность результата измерения. К недостаткам метода можно отнести то, что он требует использования регулируемой меры.
Метод компенсации погрешности по знаку предусматривает измерение с двумя наблюдениями, выполненными так, чтобы постоянная систематическая погрешность, известная по природе, но неизвестная по величине, входила в результат каждого из них с противоположными знаками. Погрешность исключается при вычислении среднего арифметического значения измеренной величины. Метод может применяться лишь в случае погрешностей, источники которых имеют направленное действие. Пользуясь этим методом, устраняют влияние на результат измерения погрешностей, вызванных влиянием постоянных магнитных полей, термо-ЭДС, явлениями гистерезисного характера - магнитным гистерезисом в ферромагнитных материалах, механическим гистерезисом в упругих материалах и т.д.
Пример – измерение ЭДС потенциометром постоянного тока. Измерение проводится дважды для устранения влияния термоэлектрической ЭДС. При первом наблюдении уравновешивают измеряемую ЭДС и измеряют значение Е1. Затем изменяют направление рабочего тока в потенциометре, вновь уравновешивают измеряемую ЭДС и измеряют значение Е2. Полученные значения содержат систематическую погрешность Dс, входящую в результаты с противоположными знаками: Е1 = Е + Dс, Е2 = Е - Dс. Значение измеряемой величины Е рассчитывается по формуле
Метод противопоставления - метод, при котором измерение проводится с двумя наблюдениями, проводимыми так, чтобы возникновение постоянной погрешности оказывало разные, но известные по закономерности воздействия на результаты наблюдений. Метод противопоставления фактически является разновидностью метода компенсации погрешности по знаку.
 |
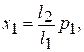Пример – способ взвешивания Гаусса. Сначала взвешиваемый груз, установленный на одной из чаш весов, уравновешивают с помощью гири р1, установленной на другой чаше:
 |
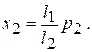где l1, l2 - длина плеч коромысла весов; х1 - измеряемая масса.
Затем переставляют груз на ту чашу, где были гири, а гири - на ту чашу, где была измеряемая масса, и вновь уравновешивают весы:
Если отношение l1/l2 не точно равно единице, то х1 ¹ х2, т.е. равновесие будет наблюдаться при различных гирях.
Исключив путем перемножения из этих двух уравнений отношение l1/l2, находят массу тела:
Пример – с помощью моста постоянного тока измеряется сопротивление Rx сравнением с известным сопротивлением R1, включенным в плечо сравнения, и сопротивлениями R3, R4, включенными в плечи отношения
.
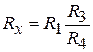Затем меняют местами сопротивления Rx, R1 и вновь, уравновесив мост резистором R1, проводят измерение. Получают результат
.
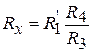Перемножив эти уравнения, получают уточненное значение:
Если R1 незначительно отличается от R1', то приближенно
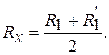
Метод противопоставления применяется, в основном, для исключения погрешности при сравнении измеряемой величины с мерой примерно равного значения.
Метод симметричных наблюдений состоит в том, что несколько наблюдений выполняют через равные интервалы времени и затем вычисляют среднее арифметическое значение симметрично расположенных наблюдений. Используется для выявления и исключения прогрессивной погрешности, являющейся линейной функцией времени или другой величины.
Пример – устранение погрешности измерения напряжения с помощью потенциометра постоянного тока (рис. 5.3), возникающей при уменьшении напряжения источника питания Б, создающего рабочий ток. Если рабочий ток потенциометра изменяется линейно во времени, то для устранения погрешности, вызванной этим изменением, достаточно выполнить три наблюдения, разделенных во времени. Сначала гальванометр Г включают в цепь нормального элемента Е0 (переключатель в положении 1) и, регулируя рабочее сопротивление Rр, добиваются уравновешивания Е0 с падением напряжения на образцовом сопротивлении R0I. Так как ток I постепенно уменьшается, можно записать
Е0= (I + k1)R0.
Затем переключатель устанавливают в положение 2, регулировкой сопротивления Rx уравновешивают падение напряжения на сопротивлении Rx и напряжение Ех, измеряют
Ех = (I + k2)Rх.
Если переключатель вновь установить в положение 1 и попытаться
 |
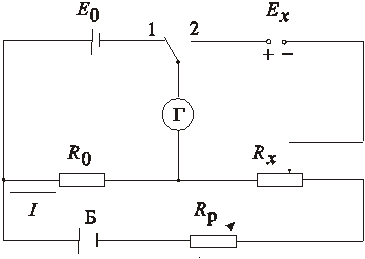Рис. 5.3. Схема потенциометра постоянно тока
уравновесить падение напряжение на образцовом сопротивлении R0 с напряжением Е0, то равновесие будет наблюдаться при других значениях рабочего тока и сопротивления R0':
Е0= (I + k3)R0'.
Для линейной зависимости погрешности от времени, при снятии показаний через равные интервалы времени, справедливо соотношение (k1+ +k3)/2 = k2. С учетом данного соотношения после соответствующих преобразований получим выражение для Ех без прогрессивной погрешности:
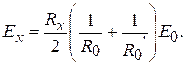
Хорошие результаты дает использование метода рандомизации, состоящего в переводе систематических погрешностей в случайные. Для этого необходимо выполнить наблюдения так, чтобы погрешности наблюдений были разнообразными и похожими на случайные.
Пример – проведение наблюдений с помощью не одного, а множества различных приборов, с привлечением различных наблюдателей, различных мест проведения измерений и т.д.
3. Внесение известных поправок в результат измерения
Внесение известных поправок в результат измерения - исключение погрешностей вычислением.
Поправка по величине равна систематической погрешности и противоположна ей по знаку. Величину поправки можно определить, в частности, используя метод сличения, сравнивая показания средства измерения с показаниями образцового прибора либо со значением меры в условиях, аналогичных условиям проведения измерения.
Некоторые систематические погрешности могут быть рассчитаны, если известны характер и особенности использованных средств и методов измерений. В частности, погрешность от влияния температуры может быть рассчитана на основании известных температурных зависимостей параметров средств измерений.
Переменная систематическая погрешность в инженерных расчетах может быть выявлена графическим методом. Для этого на одну ось наносятся точки с координатами, выражающими значения результатов наблюдений, а на другую ось – моменты времени их получения. Полученные точки соединяют плавной кривой, выражающей тенденцию изменения результатов измерения. Далее проводится анализ полученных результатов. Особенно эффективным является этот метод при линейной зависимости погрешности от времени. Так, если априорно известно, что при измерении постоянной величины Х0 систематическая погрешность изменяется линейно во времени, т.е. подчиняется зависимости х = Х0 + kt, где k – постоянный коэффициент, то для ее исключения достаточно провести два измерения х1 и х2 в моменты времени t1 и t2 (рис. 3.4). Коэффициент k вычисляется по формуле
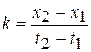. (5.1)
Зная k для произвольного момента времени ti, можно рассчитать систематическую погрешность и учесть ее в виде поправки к результату измерения.
Для нахождения изменяющейся во времени систематической погрешности могут быть привлечены и статистические методы, в частности, способ последовательных разностей. В этом способе вначале необходимо опреде-
 |
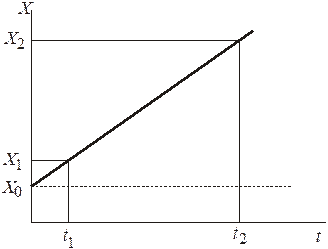Рис. 5.4. Линейное изменение систематической погрешности во времени
лить дисперсию результатов наблюдения по формуле
s2 = 
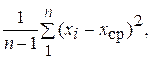(5.2)
затем, с вычислением суммы квадратов последовательных разностей результатов наблюдений, по формуле
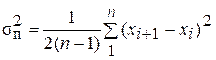. (5.3)
Идея способа состоит в том, что если переменная систематическая погрешность присутствует в результатах наблюдений, то s2 будет завышена. В то же время систематическая погрешность существенно меньше скажется на значениях последовательной разности (xi+1 – xi).
Рассчитав отношение дисперсий результатов наблюдений
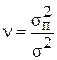
и сравнив полученный результат с критерием Аббе , можно сделать вывод о том, присутствует периодическая систематическая погрешность в результатах или нет. Если рассчитанное значение n меньше критерия Аббе nq, при заданном уровне значимости q и числе наблюдений n (n < nq), то можно сделать вывод о том, что периодическая систематическая погрешность присутствует.
Если выяснится, что имеется возрастающая или убывающая погрешность, то она должна быть количественно оценена и учтена в результатах наблюдений.
Часто применяются поправочные множители, на которые умножаются результаты измерения. Высокая точность исправленного результата измерения может быть получена лишь при условии, что поправка мала по сравнению с измеренным значением или поправочный множитель близок к единице.
3. Оценка границ систематических погрешностей
Исключение погрешностей устранением источников погрешностей, а также внесением поправок в результат измерения дает хорошие результаты, но, к сожалению, невозможно в полной мере устранить все систематические погрешности. Часто даже для хорошо изученных средств измерений и условий проведения измерений не удается внести поправки в результат. Так, для интегрирующих измерительных приборов, представителем которых является, например, индукционный счетчик электрической энергии, систематическая погрешность в значительной мере зависит от токов, потребляемых нагрузкой, причем зависимость погрешности от нагрузки имеет ярко выраженный нелинейный характер. Если представить себе ситуацию, при которой счетчик измерял бы энергию при неизменных потребляемых мощностях, то в этом случае теоретически возможно было бы внести известную поправку в результат измерения. Но такой режим работы счетчика электрической энергии практически маловероятен, чаще всего нагрузка носит переменный характер и, соответственно, систематические погрешности также будут непостоянными. Влияющие величины в процессе измерения могут изменяться, и систематические погрешности, являющиеся их следствием, сложно отследить.
Таким образом, полное исключение систематических погрешностей практически невозможно, какая-то часть погрешности остается неустраненной, поэтому следует определять границы доверительного интервала неисключенных остатков систематической погрешности. Приведем порядок нахождения границ систематических погрешностей.
Величина неисключенного остатка погрешности, вызванного i-й влияющей величиной, определяется неточностями измерения этой величины и определения ее коэффициента влияния.
Если неисключенная систематическая погрешность имеет место только у одной из составляющих и известен лишь один источник погрешности, то неисключенную систематическую погрешность результата определяют границами этой погрешности:
-Dс1 £ Q £ Dс1 . (5.4)
Распределение элементарных систематических погрешностей принято считать равномерным. При наличии нескольких неисключенных систематических погрешностей суммарную границу неисключенной систематической погрешности результата измерения можно вычислить по формуле
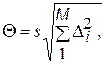
(5.5)
где M - число элементарных неисключенных систематических погрешностей; s - поправочный коэффициент, значения которого для различных вероятностей приведены в табл. П2 Прилож.
При малом числе слагаемых (2 ... 3) вычисленное по формуле (3.5) значение может превысить арифметическую сумму Dсi, что противоречит физическому смыслу. Поэтому при малом числе слагаемых систематической погрешности следует сравнить значение, найденное по формуле (3.5), с арифметической суммой слагаемых и в качестве оценки границы результирующей не исключенной систематической погрешности принять наименьшее. Таким образом,
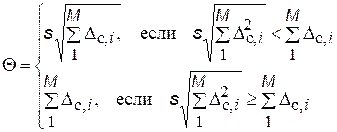
(5.6)
Поможем написать любую работу на аналогичную тему