Способы уменьшения систематических погрешностей - Дисциплина метрология – шпаргалки к экзамену.

         Так как систематические погрешности являются детерминированными величинами, уменьшение или даже полное исключение их возможно на всех этапах измерительного эксперимента. Способы исключения систематических погрешностей можно разделить на три основные группы:

устранение источников систематических погрешностей до начала измерений (профилактика систематических погрешностей);

исключение систематических погрешностей в процессе измерения с использованием специальных методов (экспериментальное исключение систематических погрешностей);

внесение известных поправок в результат измерения (исключение систематических погрешностей математическим путем).

Рассмотрим эти способы.

Устранение источников систематических погрешностей до начала измерений. Этот способ исключения систематических погрешностей является наиболее рациональным, так как он полностью или частично освобождает от необходимости устранять погрешности в процессе измерения или вычислять результат с учетом поправок. Другими словами, устранение источников систематических погрешностей существенно упрощает и ускоряет процесс измерения.

Способ может включать в себя: выбор таких методов, средств измерений, планов проведения экспериментов, которые обеспечивали бы минимальные систематические погрешности; тщательную установку нулевых показаний и калибровку средств измерений; прогрев средств измерений в течение времени, указанного в инструкции по эксплуатации; применение при сборке коротких соединительных проводов, а на сверхвысоких частотах - коаксиальных кабелей; применение в необходимых случаях экранирования и термостатирования; правильное размещение средства измерений (установка в рабочее положение, размещение вдали от источников тепла и электромагнитных полей и т.п.); применение только предварительно поверенных средств измерений и т.д.

Исключение систематических погрешностей в процессе измерений. Этот способ является эффективным путем исключения ряда систематических погрешностей. При этом нет необходимости применять какие-либо специальные установки и приспособления. Как правило, это методы измерений, позволяющие не только исключать систематические погрешности, но и оценить их.

Метод замещения. Этот метод измерений является одной из модификаций метода сравнения, которые рассмотрены в 3.2.

Метод компенсации погрешности по знаку.

Пусть x1 и x2 - результаты двух измерений; Δs - систематическая погрешность, природа которой известна, но неизвестно ее значение; хд - значение измеряемой величины, свободное от данной погрешности. Тогда х1 = хд + Δs; x2 = хд - Δs. Среднее значение равно

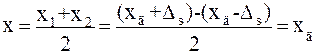
Пользуясь методом компенсации погрешности по знаку, можно исключить систематические погрешности, вызванные явлениями гистерезисного характера (магнитный гистерезис в ферромагнитных материалах, механический гистерезис в упругих материалах и т.п.).

Метод изменения знака входной величины.

x1=xд+Δs ; x2= -xд+Δs ;

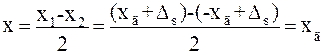
       Метод, например, может применяться в компенсаторах постоянного тока для исключения погрешности от термо- и контактных э.д.с. Здесь используется то обстоятельство, что знак термо- и контактных э.д.с. не зависит от знака измеряемого и питающего напряжений.

        Метод противопоставления. Этот метод имеет большое сходство с методом компенсации погрешности по знаку. Он заключается в том, что измерения проводят два раза, причем так, чтобы причина, вызывающая погрешность при первом измерении, оказала противоположное действие на результат второго.

        В качестве примера может служить взвешивание на равноплечих весах (способ, предложенный Гауссом для исключения погрешности вследствие остаточной неравноплечести).

При первом взвешивании массу Мх, помещенную на одну чашку весов, уравновешивают гирями с общей массой M1, помещенными на другую чашку. Тогда

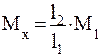,                                                (6.7)

где l2/l1 - действительное отношение плеч.

Затем взвешиваемую массу перемещают на ту чашку, где находились гири, а гири - на ту, где находилась масса. Так как отношение плеч l2/l1  не точно равно единице, равновесие нарушится и для уравновешивания массы Мх придется использовать гири с общей массой М2:

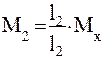.                                                  (6.8)

Разделив равенство (6.7) на выражение (6.8), получим

Mx=M1·M2                                                     (6.9)

или, если Ml и М2 лишь немногим отличаются друг от друга,

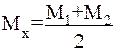.                                           (6.10)

Это выражение и равенство (6.5) одинаковы. Однако равенство (6.5), получаемое для метода компенсации погрешности по знаку, точно отражает сущность исключения погрешности. В данном же случае формула является приближенной.

Если сравнить оба метода в их математическом выражении, то можно обнаружить, что в способе компенсации погрешности по знаку погрешность, подмостах для измерения параметров электрических цепей, главным образом, при измерении электрического сопротивления на постоянном токе.

       Метод периодических наблюдений. В случае периодических погрешностей действенным методом исключения последних является метод периодических наблюдений, основанный на наблюдениях четного числа раз через полупериоды. Периодическая погрешность изменяется по закону

Δs(t) = A·sin(2·π·t/T),                                     (6.11)

       Следовательно, периодическая погрешность исключается, если взять среднее из двух наблюдений, произведенных одно за другим через интервал, равный полупериоду независимой переменной t, определяющей значение периодической погрешности. То же будет и для множества пар подобного рода наблюдений.

- Метод симметричных наблюдений. Используется для исключения прогрессирующей погрешности, которая изменяется по линейному закону, например, пропорционально времени.

E1=Ux+k·t1 ;        E2=Ux+k·t2 ,                             

где t1 и t2 - интервалы времени между регулировкой рабочего тока и наблюдениями;

k – коэффициент пропорциональности между погрешностью измерения и временем, E1 и Е2 - результаты наблюдений.

Отсюда

 .                                              

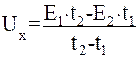Метод рандомизации. Эффективным способом уменьшения систематических погрешностей является их рандомизация, т.е. перевод в случайные. Пусть, например, имеется n однотипных приборов с систематической погрешностью одинакового происхождения. Если для данного прибора эта погрешность постоянна, то от прибора к прибору она изменяется случайным образом. Поэтому измерение одной и той же величины всеми приборами и усреднение результатов полученных наблюдений позволяют значительно уменьшить эту погрешность. Того же эффекта можно добиться, изменяя методику и условия эксперимента или те параметры, от которых не зависит значение измеряемой величины, но зависят систематические погрешности ее измерения.