Результат любого измерения отличается от истинного значения измеряемой величины в силу следующих причин:
- несовершенство средств измерений,
- некорректное применение средств измерений, в результате которого могут изменяться свойства объекта,
- воздействие на средство измерений разнообразных мешающих факторов, называемых влияющими величинами.
Влияющая величина (influence quantity) - величина, оказывающая влияние на результаты и на погрешности измерений, но не являющаяся измеряемой.
Предположим вначале, что измеряемая величина не изменяется во времени, а ее истинное значение есть x. Пусть
результат измерения, тогда разность 
есть абсолютная погрешность результата измерений.
Истинное значение измеряемой величины, конечно, неизвестно. Поэтому в последующем тексте этот термин используется в качестве модельного понятия, которое участвует в описании математической модели измерений и погрешностей измерений.
Абсолютная погрешность результата измерений (absolute error) - разность между результатом измерения и истинным значением измеряемой величины, выражается в единицах измеряемой величины.
Значение абсолютной погрешности не может быть определено в виде числа из-за того, что истинное значение x измеряемой величины неизвестно. По этой причине результат каждого измерения содержит неустранимую неопределенность значения измеряемой величины, и поэтому на практике может идти речь только об оценке каких-либо характеристик погрешности измерений, но не значений погрешности. Наиболее распространенной характеристикой погрешности является интервал 
, ограниченный предельными или предельно допускаемыми значениями. Обычно принимают 
, то ест считают этот интервал симметричным относительно нуля: 
.
В общем случае погрешность измерения Dx может содержать систематическую и случайную составляющие.
Систематическая составляющая погрешности, систематическая погрешность) - погрешность, значения которой остаются неизменными при повторных измерениях одной и той же неизменной измеряемой величины в одинаковых условиях.
Случайная составляющая погрешности, случайная погрешность - погрешность, значения которой изменяются случайным образом при повторных измерениях одной и той же неизменной измеряемой величины в одинаковых условиях.
При многократном измерении величины, истинное значение которой равно x, результаты измерений будут попадать на ось с различной плотностью, которая будет определяться характером случайной составляющей погрешности. Обычно с наибольшей плотностью результаты измерений группируются вблизи значения 
, где 
- систематическая составляющая погрешности измерений. В этом случае вид кривой, описывающей плотность распределения результатов измерений, будет иметь колоколообразный вид, как это показано в правой части рис. 4 а. Пусть - один из результатов измерений. В соответствии с определением абсолютной погрешности мы можем заключить, что форма плотности распределения 
, представленной в левой части рис. 4 а, должна повторять форму плотности распределения результатов измерений. Тогда можно назначить такие границы (-
, £), чтобы интервал, лежащий между ними содержал сумму обеих составляющих погрешности с вероятностью 
. Этот интервал представлен графически в левой части рис. 4 а, а его математическая запись имеет вид:
P(-£ Dx £) = ,
где есть не что иное, как характеристика общей абсолютной погрешности результата измерения, P(·) - вероятность события, обозначенного в скобках.
В этой ситуации из правой части рис. 4 а видно, что по результату однократного измерения об истинном значении измеряемой величины можно
заключить, что с этой же вероятностью оно находится в пределах
(-,+), то есть
P(-£ x £+) = .
Если при измерениях существует возможность определить систематическую погрешность и внести в результат поправку на нее, то интервалом неопределенности достаточно характеризовать только случайную составляющую, как это показано на рис. 4 б. В этом случае ширина интервала, содержащего погрешность, уменьшается. Интервал неопределенности истинного значения измеряемой величины определяется выражением
P(--£ x £-+) = .
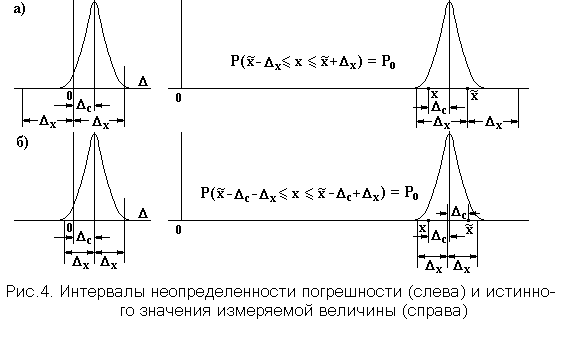
Однако, точное определение систематической погрешности невозможно, и после ее исключения всегда остается неисключенная часть систематической погрешности. Если предельное значение модуля неисключенной систематической погрешности обозначить через , то тогда и после введения поправки на систематическую погрешность интервал неопределенности результата измерения будет определяться так, как показано на рис. 4 а, где в этом случае - это предельное значение модуля неисключенной систематической погрешности измерений, которое входит в характеристику общей погрешности измерений.
Итак, если погрешности имеют случайный характер, то этому интервалу сопоставляется вероятностная мера , близкая к единице (от 0.8 до 0.95). Именно такая трактовка характеристики погрешности измерений содержится в определении термина “единство измерений”, которое приведено выше в п. 1.1.
Повторим еще раз, что указанная интервальная характеристика погрешности результата измерения есть не что иное, как интервальная характеристика остаточной неопределенности значения измеряемой величины.
Характеристика погрешности есть основная характеристика качества результата измерения и остаточной неопределенности значения измеряемой величины. Результат каждого измерения должен сопровождаться оценкой этой характеристики.
Форма выражения характеристики погрешности может быть двоякой: в виде предельного значения абсолютной погрешности, либо в виде предельного значения 
относительной погрешности, где = /x.
Относительная погрешность результата измерений (relative error)- отношение абсолютной погрешности результата измерений к истинному значению измеряемой величины, выражается в относительных единицах или в процентах.
Поскольку истинное значение измеряемой величины неизвестно, относительная погрешность вычисляется по отношению к результату измерения. Покажем, что такая замена в большинстве случаев допустима, ибо она приводит к изменению значения погрешности на величину второго порядка малости по сравнению с погрешностью: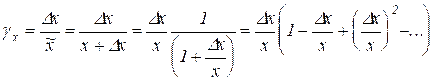 
= 
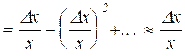
Поможем написать любую работу на аналогичную тему