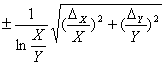ОБРАБОТКА ПОГРЕШНОСТЕЙ.

Если результат измерения определяется как совместное измерение, тогда погрешность результата можно определить воспользовавшись таблицей:

Описанные причины возникновения погрешностей определяются совокупностью большого числа факторов, под влиянием которых складывается суммарная погрешность измерения - см. формулу (1). Их можно объединить в две основные группы.

1. Факторы, постоянные или закономерно изменяющиеся в процессе измерительного эксперимента, например плавные изменения влияющих величин или погрешности применяемых при измерениях образцовых мер. Составляющие суммарной погрешности (1), определяемые действием факторов этой группы, называются систематическими погрешностями измерения. Их отличительная особенность в том, что они остаются постоянными или закономерно изменяются при повторных измерениях одной и той же величины. До тех пор, пока систематические погрешности больше случайных, их зачастую можно вычислить или исключить из результатов измерений надлежащей постановкой опыта.

2. Факторы, проявляющиеся весьма нерегулярно и столь же неожиданно исчезающие или проявляющиеся с интенсивностью, которую трудно предвидеть. К ним относятся, например, перекосы элементов приборов в их направляющих, нерегулярные изменения моментов трения в опорах, малые флюктуации влияющих величин, изменения внимания операторов и др.

Доля, или составляющая, суммарной погрешности измерения (1), определяемая действием факторов этой группы, называется случайной погрешностью измерения. Ее основная особенность в том, что она случайно изменяется при повторных измерениях одной и той же величины.

При создании измерительной аппаратуры и организации процесса измерения в целом интенсивность проявления большинства факторов данной группы удается свести к общему уровню, так что все они влияют более или менее одинаково на формирование случайной погрешности. Однако некоторые из них, например внезапное падение напряжения в сети электропитания, могут проявиться неожиданно сильно, в результате чего погрешность примет размеры, явно выходящие за границы, обусловленные ходом эксперимента в целом. Такие погрешности в составе случайной погрешности называются грубыми. К ним тесно примыкают промахи - погрешности, зависящие от наблюдателя и связанные с неправильным обращением со средствами измерений, неверным отсчетом показаний или ошибками при записи результатов.

Таким образом, мы имеем два типа погрешностей измерения:

• систематические погрешности, остающиеся постоянными или закономерно изменяющиеся при повторных измерениях.
• случайные (в том числе грубые погрешности и промахи), изменяющиеся случайным образом при повторных измерениях одной и той же величины;

В процессе измерения оба вида погрешностей проявляются одновременно, и погрешность измерения можно представить в виде суммы:

                                                              (1)

где δс- случайная, а δ- систематическая погрешности.

Для получения результатов, минимально отличающихся от истинных значений величин, проводят многократные наблюдения за измеряемой величиной с последующей математической обработкой опытных данных. Поэтому наибольшее значение имеет изучение погрешности как функции номера наблюдения, т. е. времени D(t). Тогда отдельные значения погрешностей можно будет трактовать как набор значений этой функции:

                                   (2)

В общем случае погрешность является случайной функцией времени, которая отличается от классических функций математического анализа тем, что нельзя сказать, какое значение она примет в момент времени t. Можно указать лишь вероятности появления ее значений в том или ином интервале.

Предположим, что δ(ti)=0, т.е. систематические погрешности тем или иным способом исключены из результатов наблюдений, и будем рассматривать только случайные погрешности, средние значения которых равны нулю в каждом сечении. Предположим далее, что случайные погрешности в различных сечениях не зависят друг от друга, т.е. знание случайной погрешности в одном сечении как ординаты одной реализации не дает нам никакой дополнительной информации о значении, принимаемом этой реализацией в любом другом сечении. Тогда случайную погрешность можно рассматривать как случайную величину, а ее значения при каждом из многократных наблюдений одной и той же физической величины - как ее эмпирические проявления, т.е. как результаты независимых наблюдений над ней.

В этих условиях случайная погрешность измерений dc определяется как разность между исправленным результатом Х измерения и истинным значением А измеряемой величины:

,                                                 (3)

причем исправленным будем называть результат измерений, из которого исключены систематические погрешности.

При проведении измерений целью является оценка истинного значения измеряемой величины, которое до опыта неизвестно. Результат измерения включает в себя помимо истинного значения еще и случайную погрешность, следовательно, сам является случайной величиной. В этих условиях фактическое значение случайной погрешности, полученное при поверке, еще не характеризует точности измерений, поэтому не ясно, какое же значение принять за окончательный результат измерения и как охарактеризовать его точность.

Ответ на эти вопросы можно получить, используя при метрологической обработке результатов измерения методы математической статистики, имеющей дело именно со случайными величинами.

Критерий Аббе. Применяется для обнаружения изменяющейся во времени систематической погрешности и состоит в следующем. Дисперсию результатов наблюдений можно оценить двумя способами: обычным

И вычислением суммы квадратов последовательных ( в порядке проведения измерений ) разностей (xi+1+ xi )2

Если в процессе измерений происходило смещение центра группирования результатов наблюдений, т.е. имела место переменная систематическая погрешность, то σ2 дает преувеличенную оценку дисперсии результатов наблюдений. Это объясняется тем, что на σ2 влияют вариация x. В то же время изменения центра группирования x весьма мало сказываются на значениях последовательных разностей di = xi+1 - xi , поэтому смещения x почти не отразятся на значении Q2 .

Отношение v= Q2 /   σ2   является критерием для обнаружения систематических смещений центра группирования результатов наблюдений. Критическая область для этого критерия (критерий Аббе) определяется как P(v<vq)= q, где q=1-P – уровень значимости , P – доверительная вероятность. Если полученное  значение критерия Аббе меньше vq при заданных q и n, то гипотеза о постоянстве центра группирования результатов наблюдений отвергается, т.е. обнаруживается переменная систематическая погрешность результатов измерений.

Дисперсионный анализ (критерий Фишера). В практике измерений часто бывает необходимо выяснить наличие систематической погрешности результатов наблюдений, обусловленной влиянием какого-либо постоянно действующего фактора, или определить, вызываю ли изменения этого фактора систематическое смещение результатов измерений. В данном случае проводят многократные измерения, состоящие из достаточного числа серий, каждая из которых соответствует определенным ( пусть неизвестным, но различным ) значениям влияющего фактора. Влияющими факторами, по которым производится объединение результатов наблюдений по сериям, могут быть внешние условия ( температура, давление и т.д. ), временная последовательность проведения измерений и т.п.

После проведения N измерений их разбивают на s серий (s>3) по nj  результатов наблюдений (snj = N) в каждой серии и затем устанавливают, имеется или отсутствует систематическое расхождение между результатами наблюдений в различных сериях. При этом должно быть установлено, что результаты в сериях распределены нормально. Рассеяние результатов наблюдений в пределах каждой серии отражает только случайные влияния, характеризует лишь случайные погрешности измерений в пределах этой серии.

Характеристикой совокупности случайных внутри серийных погрешностей будет средняя сумма дисперсий результатов наблюдений, вычисленных раздельно для каждой серии, т.е.

где 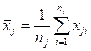 ; xji – результат i-го измерения в j-й серии.

Критерий Вилкоксона. Если закон распределения результатов измерений неизвестен, то для обнаружения систематической погрешности применяют статистический критерий Вилкоксона.

Из двух групп результатов измерений x1, x2, …, xn; y1, y2 , …, ym располагают в порядке их возрастания и приписывают им ранги – порядковые номера членов вариационного ряда. Различие средних значений каждого из рядов можно считать допустимым, если выполняется неравенство

где Ri – ранг (номер) члена xi, равный его номеру в вариационном ряду; Tq-  и  Tq+ - нижнее и верхнее критические значения для выбранного уровня значимости q.