Погрешности измерений - Ответы на вопросы по метрологии

Погрешность измерения  - это отклонение результата измерения от истинного значения величины.

Истинное значение – это значение физической величины, которое идеальным образом отражало бы в качественном и количественном отношениях соответствующие свойства объекта.

Точность измерения – качество измерений, отражающее близость к нулю систематических погрешностей результатов.

Достоверность измерений – степень доверия к результатам измерений.

Сходимость измерений – качество измерений, отражающее близость друг к другу результатов измерений, выполняемых в одинаковых условиях.

Воспроизводимость измерений – качество измерений, отражающее близость друг к другу результатов измерений, выполняемых в различных условиях.

Результат измерений всегда имеет погрешность.

По способу выражения погрешности подразделяются:

- абсолютная  (∆А) – разность между результатом измерений Аизм и действительным значением измеряемой величины Адейст

∆А = Аизм - Адейст

- относительная (δА) – это отношение абсолютной погрешности к действительному значению измеряемой величины

δА = ∆А/Аизм ≈ ∆А/Адейст

По условиям измерений погрешности подразделяются:

- основные, возникающие при измерениях произведенных при условиях, принятых за нормальные: температура +20±5 ºС, относительная влажность 65±15 %, давление 100000±4000 Па;

- дополнительные, возникающие при измерениях произведенных при условиях, отличных от нормальных.

По характеру проявления погрешности подразделяются:

- систематические, остающиеся постоянными (или закономерно изменяющиеся) при повторных измерениях тем же способом и средствами;

- случайные, изменяющиеся случайным образом при повторных измерениях одной и той же величины.

ПРОМАХИ – это грубые ошибки, обусловленные неправильным отсчетом или расчетом, небрежностью измеряющего и т.п., которые в ряде измерений не учитываются. Для суждения о том, можно ли отнести какой-то результат измерений к промахам, часто применяют правило «трех сигм». Под величиной сигма (σ) понимается среднее квадратическое отклонение случайной величины Аn от ее среднего значения Аср:

σ = ±(1/√n-1)* √(А1-Аср)2 + (А2-Аср)2 + (А3-Аср)2 +…+ (Аn-Аср)2

Результат измерений, отклоняющийся от Аср больше чем на 3 σ, обычно считают промахом.

ОСНОВНАЯ погрешность для измерительных приборов определяется их классом точности (К), который указывается на шкале или в паспорте прибора. У приборов с односторонней шкалой за норму принимается отсчет при отклонении стрелки на всю шкалу, называемый номинальным (Аном):

К = 100 ∆Апред/Аном

Электроизмерительные приборы изготавливаются девяти классов точности: 0,02; 0,05; 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0.

Относительная погрешность результата измерения δизм в данном случае определяется из соотношения

δизм (%) = (∆Апред/Аном)*100 = (∆Аном/Аизм)*К

Задача 1.3.1  Определить абсолютную и относительную погрешность результатов измерения напряжения в электрической цепи, если действительное значение напряжения равно 220 В, а были получены следующие значения: 221 В; 219 В; 217 В; 256 В; 220 В. Определить были ли промахи в результате измерения. Какой из полученных результатов измерен наиболее точно

Решение:

1        Определяем абсолютную погрешность измерений

∆А = Аизм - Адейст

∆U1 = 221 – 220 = 1 В

∆U2 = 219 – 220 = - 1 В

∆U3 = 217 – 220 = - 3 В

∆U4 = 256 – 220 = 36 В

∆U5 = 220 – 220 = 0 В

2  Определяем относительную погрешность измерений

δА = ∆А/Аизм ≈ ∆А/Адейст

δU1 = 100∆U1/Uизм = 1/221 = 0,8 %

δU2 = 100∆U2/Uизм = 1/219 = 0,4 %

δU3 = 100∆U3/Uизм = 3/217 = 1,3 %

δU4 = 100∆U4/Uизм = 36/256 = 14 %

δU5 = 100∆U5/Uизм = 0/220 = 0 %

3 Определяем были ли промахи в результате проведенных измерений.

3.1 Определяем среднее арифметическое значение результатов измерений

Uср = (U1 + U2 + U3 + U4 + U5)/5

Uср = (221 + 219 + 217 + 256 + 220)/5 = 227 В

3.2 Определяем среднее квадратическое отклонение

σ = ±(1/√n-1)* √(А1-Аср)2 + (А2-Аср)2 + (А3-Аср)2 +…+ (Аn-Аср)2

σ = ±(1/√5-1)*√(221-227)2 +(219-227)2 +(217-227)2+(256-227)2+(220-227)2

σ = ± 2*√ 36 +64 +169+841+49 =  ± 68

3*σ = 3* 68 = 204

Ответ: Так как результат измерений не отклоняется от Uср больше чем на 3 σ, то промахов нет.

Задача 1.3.2 Стрелочным вольтметром с равномерной шкалой класса точности К = 1,5 и предельным значением шкалы Uк = 300 В измерены величины трех напряжений 250 В; 150 В; 75 В. Какое из указанных напряжений измерено наиболее точно?

7

Чему равна основная и относительная погрешность каждого измерения?

Построить график изменения величины относительной погрешности заданного прибора в координатах. Дать рекомендации по использованию данного прибора.

Решение:

1 Определяем относительную погрешность каждого измерения

δизм (%) = (∆Uпред/Uном)*100 = (∆Uном/Uизм)*К

δизм 1 = (300/250)*1,5 = 1,8

δизм 2 = (300/150)*1,5 = 3

δизм 3 = (300/75)*1,5 = 6

2 Определяем абсолютную погрешность каждого измерения

δизм (%) = (∆Апред/Аном)*100

∆U = δ Uизм /100

∆U1 = 1,8*250 /100 = 4,5

∆U2 = 3*150 /100 = 4,5

∆U3 = 6*75 /100 = 4,5

Результат первого напряжения U1 = 250 В измерено наиболее точно, так как относительная погрешность его меньше остальных.

Строим график изменения величины относительной погрешности заданного прибора

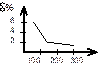
Рисунок 1.1 – График изменения величины относительной  погрешности заданного прибора

 Данный вольтметр измеряет показания достаточно близкие к предельному значению шкалы.

МЕТОДИЧЕСКАЯ  ПОГРЕШНОСТЬ  - это погрешность, возникающая в результате включения измерительных приборов в исследуемую цепь и обусловленная потребляемой ими мощностью.

Методическая погрешность, возникающая при включении амперметра.

Рисунок 1.2 – Схема включения амперметра в электрическую цепь

Iх = U/R – до включения амперметра

Iх = U/(R + RА) – после включения амперметра в цепь

δА = (I - Ix)/Ix = - (RA/R)/(1 + RA/R) – методическая погрешность.

Так как

RA/R = I2 RA/ I2 R = PA/P,

То δА = - PA/P

где РА – мощность, потребляемая амперметром;

       Р – мощность, потребляемая исследуемой цепью.

Следовательно, при измерении тока необходимо выбирать приборы, у которых потребляемая мощность значительно меньше мощности, рассеиваемой в исследуемой цепи. Поэтому необходимо, чтобы амперметр обладал как можно меньшим сопротивлением.

Методическая погрешность, возникающая при включении вольтметра.

Uх = I*R = Е*R/(R + R0), - до включения вольтметра

где Е – ЭДС источника тока;

       R0 – внутреннее сопротивление источника тока

Рисунок 1.3 – Схема включения вольтметра в электрическую цепь

После включения вольтметра напряжение будет равно

Uх = ЕRRv/(RR0+RvR0+RRv)

Тогда методическая погрешность при включении вольтметра в электрическую цепь равна

δv = (U-Ux)/ Ux = - (R/Rv)/(1+ R/Rv+ R/R0)

Учитывая, что R/Rv = Рv/Р, получаем

δv = - (Рv/Р)/(1+R/R0),

где Рv – мощность, потребляемая вольтметром;

       Р – мощность, потребляемая исследуемым резистором.

Следовательно, при измерении напряжения необходимо выбирать приборы, у которых потребляемая мощность значительно меньше мощности, рассеиваемой в исследуемой цепи. Поэтому необходимо, чтобы вольтметр обладал как можно большим сопротивлением.