Систематические погрешности, которые остаются в результатах измерений после проведения операций обнаружения, оценки и исключения, называются неисключёнными систематическими погрешностями (НСП).
В принципе любой результат измерения содержит НСП, которые образуются из многих составляющих (метода, СИ, вызванные другими источниками).
При обработке результатов измерений для определения их погрешности они суммируются со случайными, но прежде отдельные НСП должны быть просуммированы между собой для оценки доверительных границ суммарной НСП результата измерения .
При определении границ результирующей НСП ее отдельные составляющие рассматривают как случайные величины.
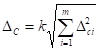При отсутствии данных о виде распределения составляющих НСП их распределения принимают за равномерные и Δс определяют из формулы
, (4.8)
где k – коэффициент, зависящий от принятой доверительной вероятности Pд, числа суммируемых НСП m и связи между отдельными составляющими; - граница i-й НСП; m – количество суммируемых НСП.
При Pд=0,9 коэффициент k=0,95, при Pд=0,95 – k=1,1, при Pд=0,99 значение k зависит от количества суммируемых НСП. Если m>4, то k=1,45, если же m≤4, то k определяют по графику зависимости k=f(m,l), где 
,
где 
- максимальная граница;
- граница, ближайшая к 
.
При практических расчетах, не требующих максимально возможной точности, можно принимать, что если m=4, то k=1,4; при m=3 – k≈1,3; при m=2 – k≈1,2.
При косвенных измерениях НСП, имеющие место при измерениях аргументов Xi, суть частные НСП результата косвенного измерения , определяемые из формулы
(4.9)
Они затем суммируются так же, как и при прямых измерениях, т.е. для определения Δс результата косвенного измерения в (4.8) необходимо подставить вместо
значения 
, вычисленные по (4.9).
Доверительную вероятность для вычисления Δс принимают такой же, что и при вычислении доверительных границ случайной погрешности результата измерения.
Поможем написать любую работу на аналогичную тему