При оценке систематических погрешностей решаются две задачи:
- нахождение поправок;
- оценивание доверительных границ неисключенных остатков систематической погрешности и их суммирование.
Поправки имеют определенные знак и значение, и их суммирование, а также учет не вызывают затруднений. Сами значения поправок находят разнообразными путями. Поправки, обусловленные систематическими погрешностями средств измерений, определяют по результатам поверок последних. Во многих случаях для этого средства измерений специально поверяют непосредственно перед применением. Поправки для учета тех или иных влияющих величин вычисляют при известных коэффициентах или функциях влияния на основе данных вспомогательных измерений этих величин. При установлении функции влияния полезны методы корреляционного и регрессионного анализа.
Вторая задача более специфична. Вне зависимости от того, к какой категории относится измерение (является ли оно прямым, косвенным, совместным или совокупным), систематическая погрешность результата оценивается, как правило, по ее составляющим, для части этих составляющих заранее известны определенные параметры, для части они вычисляются по вспомогательным данным. Так, для погрешности измерения, обусловленной основной погрешностью используемых при измерении средств, обычно известны доверительные границы. Дополнительные погрешности, обусловленные отклонением каждой из влияющих величин от ее нормального значения, определяются также в виде доверительных границ и являются примерами неисключенных остатков систематической погрешности.
Так как отдельные неисключенные остатки систематической погрешности задаются в виде доверительных границ, то их необходимо рассматривать как реализации случайных величин и суммировать методами, разработанными в теории вероятностей и математической статистике.
Математические методы суммирования случайных величин предполагают, что их функции распределений известны. Однако для неисключёных остатков систематической погрешности функции распределения, как правило, неизвестны. В этом случае можно руководствоваться следующим практическим правилом: если известна оценка доверительных границ систематической погрешности, ее распределение следует считать равномерным. Применение приведенного правила позволяет статистически суммировать погрешности и приводит к достаточно осторожным и вместе с тем не слишком завышенным оценкам суммарной неисключенной систематической погрешности.
Предположим, что доверительные границы суммарной неисключенной систематической погрешности Ds
находятся по формуле 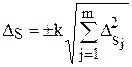 ,где
,где ![]() -доверительные границы отдельных неисключенных остатков систематических погрешностей (j =1,¼, m); k - поправочный коэффициент.
-доверительные границы отдельных неисключенных остатков систематических погрешностей (j =1,¼, m); k - поправочный коэффициент.
Так как распределение отдельных неисключенных систематических погрешностей является равномерным, то с.к.о. для них, как показано в п.5.3 , будет равно 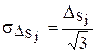 .
.
Статистическое суммирование отдельных погрешностей производится путем построения композиции их распределений. Самый простой вариант возможен при большом числе слагаемых, так как в этом случае результирующее распределение можно считать нормальным. При этом дисперсия результирующего распределения находится как сумма дисперсий составляющих.
Значение k в формуле (1.92) может быть найдено с использованием того, что результирующее распределение можно считать нормальным и оно имеет дисперсию 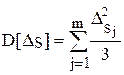 .
.
Тогда 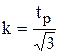 , где tP - коэффициент Стьюдента.
, где tP - коэффициент Стьюдента.
Обращаясь к таблице 1.1, нужно отметить как примечательное свойство коэффициента k, что при a<0,99 он мало зависит от числа слагаемых, т.е. можно использовать некоторые усредненные значения коэффициента k, (k » 0,95 при Р=0,90 и k » 1,1 при Р=0,95). Погрешность от применения усредненных значений к, как видно из их сравнения с точными значениями, приведенными в таблице 1.1, не превышает 10%.
Как показано в работе , значение к при Р³0,99 зависит также от соотношения между отдельными слагаемыми, особенно когда их число невелико (m£4). Зависимость k при Р=0,99 от соотношения 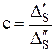 и числа отдельных слагаемых m приведена на рисунке 1.3, при этом
и числа отдельных слагаемых m приведена на рисунке 1.3, при этом ![]() -наиболее отличающееся по значению слагаемое;
-наиболее отличающееся по значению слагаемое; ![]() -ближайшее к
-ближайшее к ![]() значение другого слагаемого.
значение другого слагаемого.
При малом числе слагаемых, т.е. когда m £4, может оказаться что вычисленное по формуле (1.92) значение DS
превышает арифметическую сумму DSj, что невозможно. Поскольку всегда должно выполняться условие 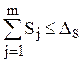 то при малом числе слагаемых (m£4) следует сравнить значение DS, найденное по формуле (1.92), с арифметической суммой слагаемых и в качестве оценки DS принять то из них, которое меньше. Таким образом, можно записать:
то при малом числе слагаемых (m£4) следует сравнить значение DS, найденное по формуле (1.92), с арифметической суммой слагаемых и в качестве оценки DS принять то из них, которое меньше. Таким образом, можно записать: 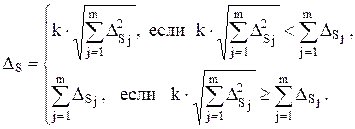
Поможем написать любую работу на аналогичную тему

