Приток жидкости в скважину. Призабойная зона скважины

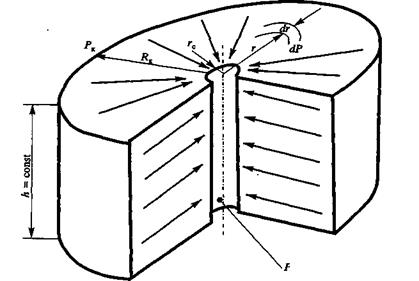
Рассмотрим задачу притока жидкости в скважину в круговом пласте, схема которого представлена на рис. 43.

Для решения задачи введем следующие допущения:

1.Пласт круговой, в центре которого расположена единственная совершенная скважина.

2.Пласт однородный и изотропный постоянной толщины.

3.Процесс течения флюида изотермический (μ = const).

4. Движение жидкости плоско-радиальное и соответствует закону Дарси.

         5.В процессе фильтрации отсутствуют любые физические и химические реакции.

Запишем уравнение Дарси:

где Q - объемный расход жидкости, м3/с; F - поверхность фильтрации, м2;

∆Р - перепад давлений, Н/м2

μ -  вязкость флюида, (Н/м2)∙с;

l - путь течения флюида, м;

k - коэффициент пропорциональности, который учитывает не только среду, в которой осуществляется фильтрация, но и все процессы взаимодействия между фильтрующимся флюидом и твердой поверхностью среды, м2.

Для схемы рис. 8.1 обозначим:

RK — радиус контура питания, м;

rс — радиус скважины, м;

h— толщина пласта, м;

Рк — давление на контуре питания, Н/м2;

Рзаб — давление на забое скважины, Н/м2.

Рис. 43. К выводу уравнения  Дюпюи

Выделим мысленно (см. рис. 1.3) на расстоянии r от оси скважины элемент пласта толщиной dr. Перепад давлений на этом элементе обозначим dP. Поверхность фильтрации для выделенного элемента такова:

                                                                                (1)

Запишем уравнение Дарси для рассматриваемой схемы:

после разделения переменных получим:

                                                             (2)          

Пределами интегрирования для уравнения, (2) являются: по Р:отРк доРзаб;

По r: от Rк до rc..    ,

Таким образом, имеем:

                                                                          (3)

После интегрирования получим

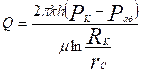                                                                                (4)

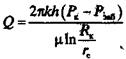Уравнение (4) называется уравнением Дюпюи и описывает приток жидкости в скважину для схемы на рис. 8.1 при принятых допущениях..                

Как видно из (4), распределение давления в дяасте вокруг работающей скважины является логарифмическим, что представлено на рис. 44.

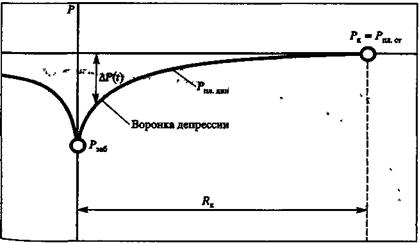
Рис 44. Распределение давления в пласте вокруг работающей скважины

Давление на контуре питания Рк является пластовым статическим давлением Рпл.ст. в дальнейшем просто Рпл (Рпл.ст - статическое пластовое давление - давление, которое существует в системе до момента отбора продукции, т.е. когда Q = 0). Давление вокруг работающей скважины в любой точке пласта (между давлением на забое скважины и давлением на контуре питания) называется динамическим пластовым давлением Рпл.дин. Динамическое пластовое давление на стенке скважины будем называть забойным давлением Рзаб. Разность между статическим и динамическим пластовыми давлениями называется депрессией АЛ:

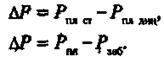                                (5)

Если линию распределения давления мысленно повернуть вокруг оси. скважины, получим так называемую воронку депрессии, Из рис. 8.1 видно, что депрессия (потери энергии при движении продукции от контура питания до стенки скважины) существенно возрастает на определенном расстоянии от стенки скважины.

Под призабойной зоной скважины (ПЗС) будем понимать зону, прилегающую к стенкам скважины, в которой существенно возрастают фильтрационные сопротивления движению продукции. До настоящего времени не существует никаких рекомендаций до численному определению радиуса этой зоны, что в значительной степени осложняет оценку эффективности различных методов искусственного воздействия да призабойные зоны скважин и сравнение их между собой.

Рассмотрим некоторые возможности численной оценки размеров ПЗС. Первая возможность базируется на аппроксимации ветвей логарифмической зависимости Р = f (r) прямыми линиями 1 и 2,

которые пересекаются в точке А (см. рис. 45). Эта точка и дает размеры (радиус) призабойной зоны скважины - rпзс  Данный прием не является единственно возможным. Численная оценка размеров призабойной зоны может быть определена и по-другому. Например, можно разбить суммарные потери энергии при движении продукции от контура питания до стенки скважины поровну, т.е. чтобы площади S1 и S2 были равны (см. рис. 46). Граница этих площадей и будет численно определять радиус ПЗС. Совершенно очевидно, что для оценки размеров ПЗС можно предложить и другие методы.

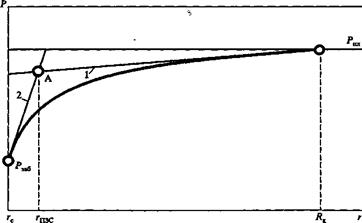
Рис. 45 Первый вариант определения радиуса ПЗС

Важно подчеркнуть: какой бы метод оценки размеров ПЗС не использовался, если возникает необходимость сравнения результатов, зависящих от размеров ПЗС, при этом сравнении необходимо в обоих случаях использовать один и тот же метод расчета размеров (радиуса) ПЗС.

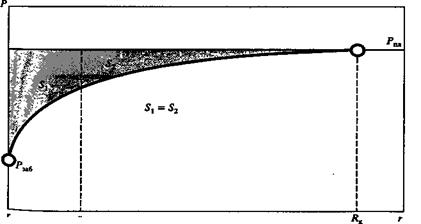
Рис. 46. Второй вариант определения радиуса ПЗС