Приток жидкости, газа, воды или их смесей к скважинам происходит в результате установления на забое скважин давления меньшего, чем в продуктивном пласте. Течение жидкости к скважинам исключительно сложно и не всегда поддается расчету. Лишь при геометрически правильном размещении скважин (линейные или кольцевые ряды скважин и правильные сетки), а также при ряде допущений (постоянство толщины, проницаемости и других параметров) удается аналитически рассчитать дебиты этих скважин при заданных давлениях на забоях или, наоборот, рассчитать давление при заданных дебитах. Однако вблизи каждой скважины в однородном пласте течение жидкости становится близким к радиальному. Это позволяет широко использовать для расчетов радиальную схему фильтрации. Уравнение распределения давления вокруг скважины:
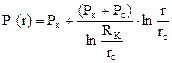
Из уравнения следует, что функция P(r) является логарифмической, т. е. давление вблизи стенок скважины изменяется сильно, а на удаленном расстоянии — слабо. Это объясняется увеличением скоростей фильтрации при приближении струек тока к стенкам скважины, на что расходуется больший перепад давления, графическое представление данной зависимости получило название «Депрессионная воронка». Формула радиального притока жидкости
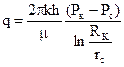
где k(мкм2) – проницаемость, h(м) – толщина пласта, μ(мПа*с) – вязкость пластового флюида.
Требуется:
1) Нарисовать линии тока при радиальной фильтрации жидкости к несовершенной по характеру и степени вскрытия пласта скважине;
2) Нарушения линейного закона фильтрации при счёт высоких скоростях фильтрации (Fинерции) и при проявлении неньютоновских свойств жидкости. В этом случае используется двучленная формула притока 
, где А – коэффициент, учитывающий силы вязкостного трения; В – коэффициент, определяющий действия сил инерции.
Поможем написать любую работу на аналогичную тему