Чтобы оценить роль притока жидкости из пласта на процесс заполнения НКТ, вероятно, исходные предпосылки можно строить без учета потерь давления на трение. Во всяком случае, соответствующую поправку можно ввести в конечной стадии по корректировочным кривым (см. рис. 3.4). При решении поставленной задачи также используется метод последовательной смены стационарных состояний, хотя по сравнению с предыдущей задачей в этом случае допускается большая условность. С учетом сказанного и в предположении линейности притока из пласта исходная система уравнений записывается следующим образом:
(3.14)
где Qпл - производительность пласта (приток); Qзатр - количество жидкости, поступающей в насос из межтрубного пространства. Остальные обозначения прежние.
Принимая во внимание, что Q = f·dl/dt и Qзатр = -fк· dlк/dt, а также
(где Lскв - глубина скважины - расстояние от устья до продуктивного горизонта; Lсп - глубина спуска насоса), систему (3.14) преобразуем в систему дифференциальных уравнений, на основании которых может быть рассчитана динамика заполнения насосно-компрессорных труб с учетом притока жидкости из пласта:
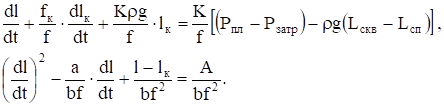(3.15)
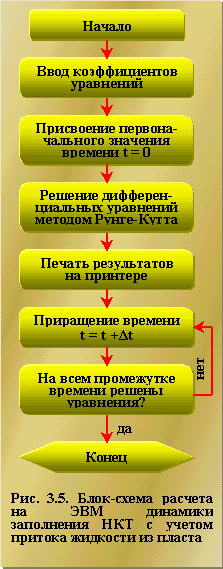Решение этой системы может быть выполнено численно на электронно-вычислительных машинах. Блок-схема расчета на ЭВМ представлена на рис. 3.5. В связи с необходимостью оперативной оценки действия химреагентов приведем экспресс-метод расчета динамики заполнения насосно-компрессорных труб l(t) и соответствующего изменения положения уровня в кольцевом пространстве lк (t).
Порядок расчета l(t) и l(t) с учетом-притока из пласта. В начальный момент времени (t = 0) l(t) = lк(t) = lo, приток из пласта отсутствует (Qпл1 = 0). Следовательно, в начальный момент времени производительность насоса Q, будет практически соответствовать нулевому напору и равняться расходу жидкости в кольцевом пространстве Q1 = Qзатр1. Изменение уровня при этом для заданного промежутка времени Δt1 будет соответственно в трубах Δl1 = Q1 ·Δt1/f, в кольцевом пространстве Δlк1 = Q1 ·Δt1/fк.
На основе вычисленных значений Δl1 и Δlк1 определяются новые положения уровня жидкости:
в трубах 
;
в кольцевом пространстве 
.
Вторым этапом расчетов определяется производительность насоса Q2 по необходимому напору H2 = lо - lк1 и приток из пласта:
Расход жидкости в кольцевом пространстве будет:
Изменение уровня:
в трубах 
;
в кольцевом пространстве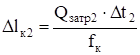 
.
Новое положение уровня:
в трубах 
;
в кольцевом пространстве 
. Следующие этапы расчета проводятся аналогичным образом. Точность расчета естественно определяется размерами задаваемого интервала времени Δt.
Расчеты показывают, что влияние притока на темп заполнения насосно-компрессорных труб независимо от производительности скважины несущественно. Небольшая погрешность (до 1%) от неучета притока возникает лишь при использовании насосов с номинальной производительностью более 500 м3/сут в весьма высокопродуктивных скважинах. Отмеченная погрешность несколько возрастает с увеличением отношения fк/f .
Незначительность влияния притока объясняется тем, что оно, по существу, сказывается на некотором уменьшении необходимого напора насоса, так как в результате работы пласта уровень в кольцевом пространстве будет снижаться несколько медленнее. Но при реальном соотношении fк/f, много меньшем единицы, абсолютное изменение в положении уровня в кольцевом пространстве незначительно. Также незначительны изменения напора насоса, а тем более его производительности, поскольку в начальный момент насос работает в области круто-падающей характеристики Q - Н.
Таким образом, наличие притока из пласта в начальный момент освоения скважины после ее остановки не оказывает заметного влияния на период заполнения насосно-компрессорных труб. В подавляющем большинстве случаев период заполнения НКТ не превышает 8-10 мин, а в остальных 15-25 мин.
Поможем написать любую работу на аналогичную тему