Определение сил давления на стенки

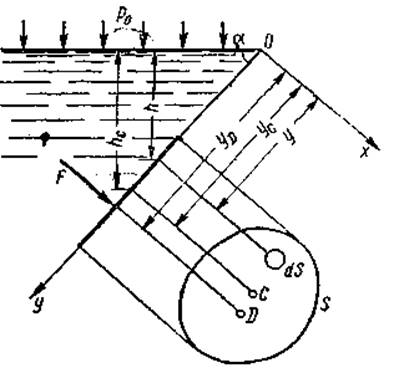
Плоская стенка имеет наклон к горизонтали под углом α.

Вычислим силу F давления действующую со стороны жидкости на некоторый участок стенки ограниченный произвольным контуром площадью S. Элементарная сила давления приложена к малой площадке d будет равна

р0- давление на свободной поверхности, h- глубина расположения площадки dA.     

проинтегрируем полученное выражение по всей площади

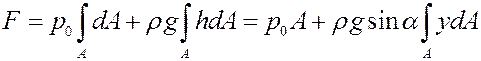
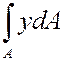     - статический момент площади относительно оси ох.

y- координата площадки dA.

Статический момент площади относительно оси ох определяют

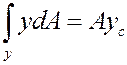
тогда сила

hc- глубина расположения центра масс площадки А.

  (1).

Таким образом полная сила давления жидкости на плоскую

Центр давления

Т.К.р0 передаётся всем точкам площади А одинаково, то его равнодействующая F0 будет приложена в центре масс площади А. Для нахождения точки приложения силы давления Fж от веса жидкости (т.Д) применим теорему механики согласно которой: момент равнодействующей силы относительно оси ох равен сумме моментов составляющих сил.

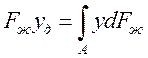    yд- координата точки приложения силы Fж.

Выразим силы Fж через координаты yc  и y и тогда получим

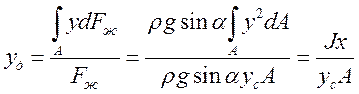
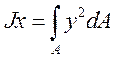    - момент инерции площади А относительно оси ох.

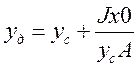      тогда (1)

Jх0- момент силы площади А относительно центральной оси параллельной х0. таким образом точка приложения силы Fж расположенной ниже центра масс стенки, расстояние между ними определяется по выражению

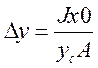(2)

если давление р0 равно атмосферному, то т.Д центр давления.

При р0> ратм центр давления находится как точка приложения равнодействующих 2х сил F0 и Fж. Чем больше F0 по сравнению с Fж , тем центр давления ближе к центру масс площади А.

В жидкости возможны лишь распределения силы, поэтому центры давления принимаются условно.

силы давления на криволинейные стенки

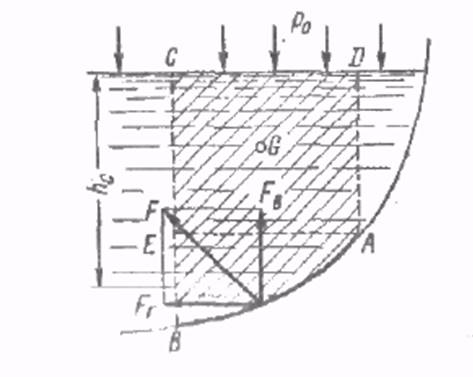
Рассмотрим цилиндрическую поверхность АВ с образующей перпендикулярной пл-ти чертежа и определим силу  давления на эту поверхность АВ. Выделим объём жидкости ограниченной поверхностью АВ. Вертикальными плоскостями проведёнными через границы этого участка и свободной поверхностью жидкости т.е. объём АВСД и рассмотрим условия его равновесия в вертик.и горизонт. направлениях.

Если жидкость действует на стенку с силой F, то стенки АВ действуют с силой F направленной в обратную сторону (сила реакции). Разложим силу реакции на 2 составляющие горизонт и вертик. Условие равновесия в вертикальном направлении:

 (1)

G- вес выделенного объема жидкости

Аг- площадь горизонтальной проекции пов-ти АВ.

Условие равновесия в гориз направлении записывается с учётом того, что силы давления жидкости на поверхностях ЕС и АД взаимно уравновешиваются. Остаётся только сила давления на ВЕ, тогда

hc- глубина расположения центра масс площади ВЕ.

Сила давления