Уравнения Эйлера и их интегралы.

Уравнения Эйлера и их интегралы.

Уравнения равновесия жидкости:

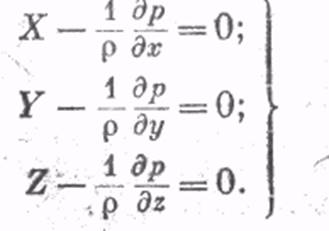
Система дифференциальных уравнений гидростатики называется уравнениями Эйлера.  

Для практического пользования удобнее вместо системы уравнений получить одно эквивалентное им уравнение, не содержащее частных производных. Для этого умножим первое из уравнений на dx, второе — на dy, третье — на dz и, сложив все три уравнения, получим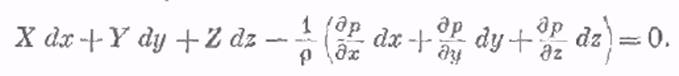

Трехчлен, заключенный в скобках, представляет собой полный дифференциал давления, т. е, функции р (х, у, z)t поэтому предыдущее уравнение можно переписать в виде:

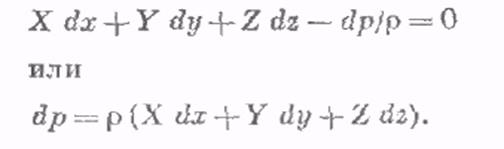
Полученное уравнение выражает приращение давления dp при изменении координат на dx, dy и dz в общем случае равновесия жидкости. Если предположить, что па жидкость действует только сила тяжести, и направить ось z вертикально вверх, то X = Y = О, Z =-g и, следовательно, вместо уравнения (1) для этого частного случая равновесия жидкости получим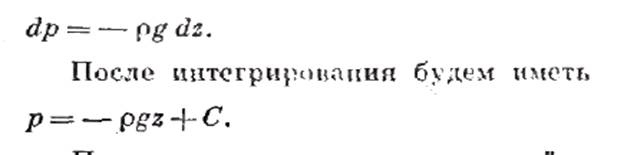                                                                   

Постоянную интегрирования найдем, подставив параметры свободной поверхности, для которой при z = z0 p = р0

Получим

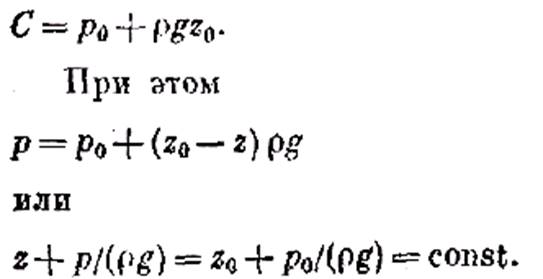
Основная формула ГИДРОСТАТИКИ.

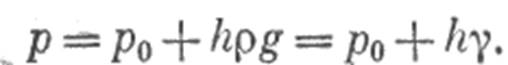
Уравнение  называют основным уравнением гидростатики; по нему можно подсчитать давление в любой точке покоящейся жидкости. Это давление, как видно из уравнения, складывается из двух величин: давления р0 на внешней поверхности жидкости и давления, обусловленного весом вышележащих слоев жидкости. Величина  р0 является одинаковой для всех точек объема жидкости, поэтому, учитывая свойство гидростатического давления, можно сказать, что давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости и по всем направлениям одинаково. Это положение известно под названием закона Паскаля. Давление жидкости, как видно из формулы (1),возрастает с увеличением глубины по закону прямой и на данной глубине есть величина постоянная.