Все тела существуют и движутся в пространстве и времени. Любое тело имеет объем, то есть пространственную протяженность в трех измерениях. Объемом тела также называют часть пространства, ограниченную данным телом. Время является мерой продолжительности и последовательности смены явлений и событий. В механике время выражает порядок смены событий, происходящих с телами.
Движением в широком смысле слова называется всякое изменение вообще. Простейшей формой движения является механическое движение, которое заключается в изменении с течением времени положения тел или их частей относительно друг друга в пространстве с течением времени.
Материальной точкой (частицей) называется тело, размерами которого можно пренебречь при описании его механического движения.
В основе классической механики лежат законы Ньютона, которые справедливы лишь для макроскопических тел, которые можно считать материальными точками, при их движении со скоростями гораздо меньше скорости света в вакууме.
Движение тела можно рассматривать только относительно какого-то другого тела. Поэтому, при описании механического движения материальной точки необходимо выбрать систему отсчета. Система отсчета - это совокупность тела отсчёта (твердое тело, относительно которого определяется положение других тел в различные моменты времени), жестко связанной с ним системой координат и синхронизированными часами для отсчета времени (показывающими нуль в начальный момент времени наблюдения движения).
Время в ньтоновской механике является однородным, поэтому начало его отсчета можно брать произвольно. В ньютоновской механике свойства пространства описываются геометрией Евклида, а ход времени одинаков во всех системах отсчета.
При движении т.М её координаты и радиус-вектор изменяются со временем. Поэтому для описания движения т.М надо указать вид функции либо её координат, либо её радиус-вектора:
или
. (2)
В СИ размерность 
.
Три уравнения (1) или эквивалентное им векторное уравнение (2) называются кинематическим уравнением движения.
Траектория точки - это линия, описываемая точкой при движении относительно выбранной системы отсчета. В зависимости от формы траектории различают прямолинейное и криволинейное движение точки.
Длина пути (путь) - это расстояние, пройденное точкой за рассматриваемое время вдоль траектории в направлении движения точки.
Вектором перемещения точки за промежуток времени от 
до 
называется приращение радиус-вектора 
за этот промежуток времени:
.
Если рассматривать достаточно малый промежуток времени 
, то можно пренебречь отличием модуля вектора перемещения 
и длиной пути 
, т. е. можно считать, что 
.
Вектор перемещения можно представить за конечной промежуток времени 
(от 
до +) через векторную сумму перемещений вдоль осей координат:
Здесь
;
;
Для характеристики направления и быстроты движения точки введём понятие вектора скорости. Средней скоростью точки в промежутке времени называется вектор
Скорость точки в момент времени есть вектор 
, равный первой производной от радиус-вектора этой точки по времени:
,
причём модуль скорости v будет
.
В СИ размерность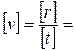 
м/с.
Модуль скорости можно определить через её проекции на оси координат следующим образом:
.
При прямолинейном движении направление скорости как вектора остаётся неизменным. Движение точки называется равномерным, если модуль её скорости не изменяется со временем, т. е.
При равномерном движении точки длина пройденного пути зависит от времени линейно:
.
В общем случае неравномерного движения пройденный путь определится как интеграл от скорости
.
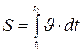Средней путевой скоростью неравномерного движения 
точки называется скалярная величена
,
где 
- длина пройденного пути данного участка траектории. Скорость 
равна модулю вектора скорости такого равномерного движения, при котором на прохождение того же пути потребуется столько же времени , как при неравномерном движении.
Для характеристики быстроты изменения вектора скорости при неравномерном движении точки введём понятие ускорения.
Средним ускорением точки в интервале времени от до 
называется вектор 
, равный отношению приращения вектора скорости 
за этот промежуток времени к его продолжительности :
.
Мгновенным ускорением точки называется векторная величина 
равная первой производной от вектора скорости или второй производной от радиус-вектора по времени:
.
Иначе, ускорение точки в момент времени есть предел среднего ускорения:
.
В СИ размерность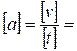 
м/с.
Ускорение, как радиус-вектор и скорость, можно представить в ортогональном базисе:
.
Рассуждая так же, как для вектора скорости, получим проекции ускорения на оси координат:
; 
.
Следовательно, модуль ускорения будет равен:
.
Если ускорение материальной точки не изменяется со временем, то такое движение называется равнопеременным. В этом случае модуль вектора скорости зависит от времени линейно:
,
где 
- модуль начальной скорости точки.
Путь при таком движении определиться как интеграл
.
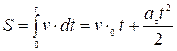Силой называется векторная величина, которая является мерой механического действия на данное тело со стороны других тел. Механическое взаимодействие может осуществляться между непосредственно контактирующими телами (например, трение, давление) или между удалёнными телами (гравитационное притяжение, электромагнитное притяжение и отталкивание). Особая форма материи, связывающая частицы вещества в единые системы и передающая с конечной скоростью действие одних частиц на другие, называется физическим полем. Каждой силе всегда соответствует некоторое тело, действующее на рассматриваемое тело с этой силой.
Сила 
полностью определена, если заданы её модуль, направление в пространстве и точка её приложения к данному телу. Прямая, вдоль которой направлена сила, называется линией действия силы.
Поле, действующее на материальную точку с силой , называется стационарным, если оно не изменяется с течением времени, т. е. 
. Для стационарности поля необходимо, чтобы создающие его тела покоились относительно выбранной инерциальной системы отсчета.
Одновременное действие на материальную точку М нескольких сил 
, 
, 
(рис. 1) эквивалентно действию одной силы (равнодействующей или результирующей), которая является векторной суммой этих сил: 
В ньютоновской механике массой 
материальной точки называется положительная скалярная величина, являющаяся мерой инертности этой точки. Под действием силы материальная точка изменяет свою скорость не мгновенно, а постепенно, т. е. приобретает конечное ускорение, которое тем меньше, чем больше масса материальной точки, т. е. 
или 
. В СИ размерность 
.
Опыт показывает, что ускорение 
, приобретаемое материальной точкой под действием силы , прямо пропорционально модулю этой силы и обратно пропорционально массе точки, причем направление ускорения совпадает с линией действия силы, т. е. 
. В системе СИ размерность 
.
Опыт показывает, что, если на материальную точку одновременно действуют несколько сил, то каждая из них сообщает точке своё ускорение, как если бы других сил не было (принцип независимости действия сил). Т. е. ускорение, приобретаемое материальной точкой под действием нескольких сил, будет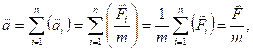 
где 
- результирующая сила.
Подставив в уравнение (1) 
получим:
. (2)
Дифференциальное уравнение (2) называют уравнением движения материальной точки. В проекциях на оси координат 
, 
, 
это уравнение примет вид:
Поможем написать любую работу на аналогичную тему