Водослив с тонкой стенкой

Рассмотрим поток, протекающий через прямоугольный водослив с тонкой стенкой, имеющей острую кромку (рис. 11.1 Водослив11.1).

Свободная поверхность воды при подходе к стенке начинает понижаться, образуется кривая спада. Это определяет условие для нахождения напора Н перед водосливом, он измеряется на расстоянии не менее 3H, т.е. там, где кривая спада становится практически незаметной. С другой стороны, сразу же после прохождения гребня водослива происходит сжатие струи. На уровне гребня водослива очертания верхней и нижней границ струи становятся почти параллельными и составляют угол 41º30/ к горизонтали, толщина струи здесь равна 0,435Н.

Расход жидкости через прямоугольный водослив с тонкой стенкой можно установить на основе закономерностей истечения жидкости через большие отверстия.

При Н1 = 0 и Н2= Н расход имеет вид

или, заменяя , где  ‑ коэффициента расхода водослива, получим

Значения коэффициента расхода прямоугольного водослива с тонкой стенкой без бокового сжатия  изменяются в пределах . Его среднее значение можно найти по толщине струи на уровне гребня водослива . Так как сжатие в этом сечении отсутствует , то, приняв коэффициент скорости , получим следующее выражение для расхода:

т. е. коэффициент расхода .

Величину коэффициента расхода основное влияние оказывает характер вертикального сжатия струи, что, в свою очередь, определяется величинами Р и H. Кроме того, на коэффициент расхода влияет еще и скорость подхода жидкости . Одной из экспериментальных зависимостей для , учитывающей указанные факторы, является формула Базена:

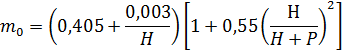
Для незатопленного прямоугольного водослива с тонкой стенкой без бокового сжатия коэффициент расхода приближенно можно определять по следующей зависимости, справедливой при  и .