Для того, чтобы вязкопластичная жидкость начала перемещаться необходимо создать между начальным и конечным сечениями участка трубы длиной некотурую разность напоров, при которой будет преодолена величина начального статического напряжения сдвига
. При этом жидкость отрывается от стенок трубы и первоначально движется на подвижном ламинарном слое, сохраняя свою прежнюю пространственную структуру, т.е. с одинаковыми скоростями по всему отсеку потока. Разрушение этой структуры происходит позже и при некотором превышении напора.
Поскольку в начальный момент времени силы трения будут возникать только у стенок трубы, то уравнения равновесия можно записать в следующем виде:
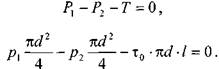
Необходимая разность напоров между началом и концом участка трубы определится следующим образом:
Таким образом, при превышении разности напоров расчётную величину жидкость начнёт двигаться по трубе, причём характер (режим) её движения будет зависеть от величины
. При движении вязкопластичной жидкости возможны три режима течения её: структурный, ламинарный и турбулентный.
Условие
является необходимым для начала движения жидкости
в структурном режиме, при этом под величиной статического напряжения сдвига следует понимать величину соответствующую длительному покою жидкости, т.е. с учётом проявления тиксотропных свойств жидкости.
Структурный режим течения жидкости предполагает наличие вдоль стенок трубы сплошного ламинарного слоя жидкости; в центральной части трубы наблюдается ядро течения, где жидкость движется, сохраняя прежнюю свою структуру, т.е. как твёрдое тело. Размеры центрального ядра течения (радиус
) может быть определён исходя из следующего соотношения: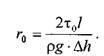
При увеличении А/г размеры ламинарной зоны будут постепенно увеличиваться за счёт уменьшения размеров ядра течения пока структурный режим не перейдёт в полностью ламинарный режим движения жидкости. В дальнейшем ламинарный режим постепенно сменится турбулентным режимом движения жидкости.
Для определения закона распределения скоростей по сечению потока при структурном режиме движения жидкости запишем некоторую функцию для касательных напряжений в соответствии с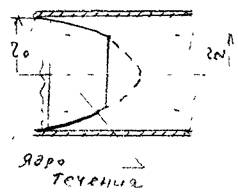 
формулой Бингама:
Тогда распределение скоростей по сечению трубы можно выразить следующим образом:
?
где: 
- касательное напряжение на стенке трубы радиуса
,
- скорость жидкости на расстоянии
от центра трубы. После интегрирования этого уравнения получим:
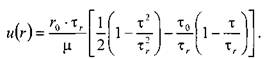
И окончательно:
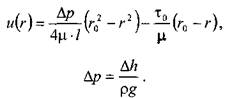
Для определения скорости в ядре течения примем
, где
- радиус ядра течения
(структурной части потока жидкости). Тогда величина скорости в этом ядре течения (скорости в ядре течения одинаковые равны)
: '
Расход жидкости при структурном движении можно определить, используя известные соотношения дл круглой трубы:
Интегрируя уравнение в пределах от
до
, получим:
5 f
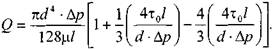
Последнее уравнение, известное как формула Букингама, можно упростить:
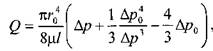
где: 
- разность давлений при начале движения жидкости, когда каса-
тельнве напряжения в ней достигают величины касательного напряжения сдвига. Если пренебречь величиной второго члена ввиду его малости, получим:
* где: 
- обобщённый критерий Рейнольдса.
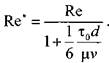
Комплексный параметр
= Sen носит название числа Сен-Венана.
Поможем написать любую работу на аналогичную тему