Метод дифференцирования

Из математического анализа известно, что прирост функции y=y(x1, x2, .....,xn) при переходе из точки А(x01,x02,.....,x0n) в точку В(x11,x12,.....,x1n) определяется как

Dy= dy + E,

где dy - дифференциал функции в точке А, Е - ошибка разложения.

Если точки А и В близки, Е является очень малой величиной, значением которой можно пренебречь. Тогда можно записать, что  Dy » dy.

Дифференциал - главная линейная часть приращения функции относительно приращения аргументов определяется как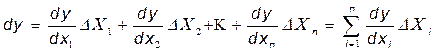

Здесь - частная производная функции y по переменной xi, вычисленная в точке А, то есть при x1=x01,x2=x02,...,xn=x0n.

- приращение переменной  xi   при переходе функции из точки А в точку В.

Dx1=x11-x01, Dx2=x12-x02, ......, Dxn=x1n-x0n.

Итак, если  Dxi®0 (то есть  В®А), то Е®0  и 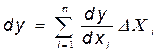                 (1.6.4)

Влияние изменения фактора xi на изменение показателя y определяется величиной

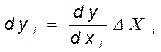
Пример 1.4.  Выручка предприятия составила В=Ц*М.

Прирост выручки

Точка А здесь I квартал, её координаты А(Ц0, М0).

Точка В - 2 квартал, В(Ц1, М1).

С учетом данных примера 1.1. получим А(2400; 12), В(2500;11)

DВрп= Ц0*DМ+ М0*DЦ= 2400(11-12) + 12(2500-2400)== -2400+1200= -1200.

Итак общее изменение выручки DВРП= -1200 тыс.тг.,

в том числе: за счет изменения цены  DВРПц= +1200 тыс.тг.,

за счет изменения физического объема  DВРПм= -2400 тыс.тг.

Напомним: равенство (1.6.4) является приближенным.

Если в примере 1.3. определить прирост показателя ВРП точно, то получим  DВРП=Ц1М1-Ц0М0=11*2500 -12*2400=27500 -28800= -1300 тыс.тг. Видно, что при использовании метода дифференцирования произошла ошибка на 100 тыс.тг. Это именно та Е, о которой говорилось ранее.

В экономических расчетах, где динамика факторов может быть существенной, значение ошибки может быть большим. Поэтому её нужно учитывать. При этом возникает две задачи:

а) как рассчитать величину этой ошибки?

б) как распределить её между отдельными факторами?

Расчет величины ошибки достаточно прост:

Е= Dy – dy ,

где Dy= y(x11,x12,..., x1n)- y(x01,x02,...,x0n), а значение dy рассчитывается по формуле (1.6.4).

Задача распределения величины ошибки (“неразложимого остатка”) между отдельными факторами решается с применением различных методов. Рассмотрим основные из них.