Компоновка сечения и расчет надкрановой части  колонны

Определение расчетных длин надкрановой части колонны

Пример 8.1. Подобрать сечение надкрановой части колонны, принимая его в виде сварного двутавра высотой hв = 700 мм (см. рис. 8.1).

Определяем расчетную длину в плоскости действия момента (относительно оси х-х):

lx2 = m2 l2 = 3 × 6,3 = 18,9 м,

где    m2 = 3,0 – коэффициент расчетной длины (при соблюдении условий

l2 /l1 = 6,3 / 14,1 = 0,45 < 0,6  и  N1 /N2 = 2473,5 / 479,3 = 5,16 > 3)

определяется по табл. 8.1 с учетом того, что при жестком сопряжении ригеля с колонной верхний конец закреплен от поворота. При других условиях m2 определяется по ;

lу2 = l2 – hб = 6,3 – 1,7 = 4,6 м.

Таблица 8.1

Коэффициенты расчетной длины m1 и m2 для

одноступенчатых колонн рам одноэтажных промышленных зданий

при l2 / l1 £ 0,6 и b = N1 / N2 ³ 3

Обозначения, принятые в таблице:

l1; I1 N1 – соответственно длина нижнего участка колонны, момент инерции сечения и действующая на этом участке продольная сила;

l2; I2; N2 – то же верхнего участка колонны.

В плоскости, перпендикулярной действию момента (относительно

оси у-у), расчетная длина lу2 принимается равной расстоянию между точками закрепления верхней части колонны от смещения перпендикулярно плоскости действия момента (такими точками являются тормозная конструкция подкрановой балки и распорки по колоннам в уровне поясов стропильных ферм):

Подбор сечения колонны

Предварительно необходимую площадь сечения определяем, используя формулу Ясинского:

Атр = N2 (1,25 + 2,8e/h)/Ry = 479,3 × (1,25 + 2,8 × 239 / 70) / 24 = 203 см2,

где    е = M2,max /N2 = 1144,6 / 479,3 = 2,39 м = 239 см – эксцентриситет продольной силы.

Распределяем площадь Атр между стенкой и полками.

Толщина стенки tw принимается в пределах (1/60 – 1/120)hw =

= 1,08 – 0,6 см, где hw = hв – 2tf  = 70 – 2 × 2,5 = 65 см (толщиной поясов предварительно задаются tf  = 12 – 30 мм, принимаем tf  = 25 мм). Назначаем tw = 10 мм.

Требуемая площадь полки

Аf = bf tf = (Атр – hwtw)/2 = (203 – 65 × 1) / 2 = 69 см2.

Ширина полки обычно назначается в пределах bf = (1/20 – 1/30)l2 =

= (1/20 – 1/30) 6300 = 315 – 210 мм. Принимаем bf  = 300 мм.

Толщина пояса

tf  = Af /bf  = 69 / 30 = 23 мм.

Окончательно проектируем стенку из листа 650×10 мм и полку из листа 300×22 мм. Размеры увязываются со стандартными размерами листов, выпускаемых отечественными заводами (см. табл. 3.7, 3.8, 3.9).

Проверка устойчивости надкрановой части колонны

1. Проверка устойчивости колонны в плоскости действия момента (относительно оси х-х).

Определяем геометрические характеристики принятого сечения колонны:

– площадь стенки

Aw = hw tw = 65 × 1 = 65 см2;

– площадь полки

Аf = bf tf  = 30 × 2,2 = 66 см2;

– площадь всего сечения

А = Aw + 2Af  = 65 + 2 × 66 = 197 см2;

– момент инерции

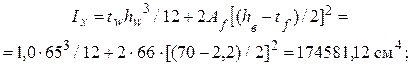
– момент сопротивления для наиболее сжатого волокна;

– радиус инерции

– гибкость стержня

– условная гибкость

– радиус ядра сечения

Проверяем устойчивость колонны в плоскости действия момента по формуле

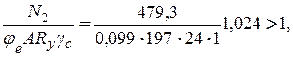
где gc = 1 – коэффициент условий работы;

jе – коэффициент устойчивости при сжатии с изгибом, определяемый в зависимости от условной гибкости `lх  и приведенного относительного эксцентриситета mef, вычисляемого по формуле

mef = h mx = 1,36 × 9,44 = 12,84,

здесь mх = е/r  = 239 / 25,32 = 9,44;

h – коэффициент влияния формы сечения, определяемый по табл. 5.8 в зависимости от типа сечения, отношения Af /Aw  и  mх.

При Af /Aw = 66 / 65 = 1,05 > 1,0; mх = 9,44 > 5 и `lх = 2,16 < 5 находим

h = 1,4 – 0,02`lх = 1,4 – 0,02 × 2,16 = 1,36.

По табл. 8.2 определяем jе = 0,099.

Таблица 8.2

Коэффициенты φe для проверки устойчивости внецентренно-сжатых

сплошностенчатых стержней в плоскости действия момента

П р и м е ч а н и я: 1.Значения коэффициента : φe в таблице увеличены в 1000 раз.

2. Значение φe принимать не выше значений φ.

Проверка показала, что надкрановая часть колонны не прошла по устойчивости.

Увеличиваем ширину полки: принимаем bf  = 320 мм.

Определяем характеристики:

Аf = bf tf  = 32 × 2,2 = 70,4 см2;

А = Aw + 2Af = 65 + 2 × 70,4 = 205,8 см2;

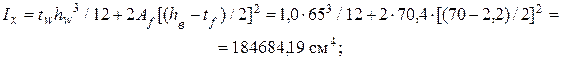
 = 5276,69 / 205,8 = 25,64 см;

mх = е / r = 239 / 25,64 = 9,32.

Находим коэффициент влияния формы сечения по табл. 5.8:

h  = 1,4 – 0,02 = 1,4 – 0,02 × 2,14 = 1,36;

mef = h mх = 1,36 × 9,32 = 12,68.

По табл. 8.2 определяем jе = 0,100.

Проверяем устойчивость колонны относительно оси х-х:

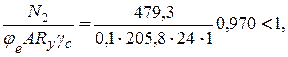
Условие выполняется.

Таблица 8.3

Коэффициенты φe для проверки устойчивости внецентренно-сжатых

сквозных стержней в плоскости действия момента

П р и м е ч а н и я: 1.Значения коэффициента : φe в таблице увеличены в 1000 раз.

2. Значение φe принимать не выше значений φ.

Недонапряжение

что допустимо для составных сечений.

2. Проверка устойчивости колонны из плоскости действия момента    (относительно оси у-у).

Во внецентренно-сжатых элементах, у которых жесткости в обоих главных направлениях различны (EIy < EIx) и момент действует в плоскости наибольшей жесткости, возможна потеря устойчивости в плоскости, перпендикулярной действующему моменту.

Определяем геометрические характеристики сечения при работе стержня относительно оси у-у:

– момент инерции сечения

– радиус инерции

– гибкость стержня

– условная гибкость

Проверку выполняем по формуле

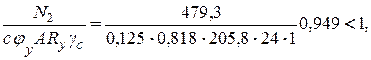
где    jy = 0,818 – коэффициент устойчивости при центральном сжатии, определенный в зависимости от условной гибкости  по табл. 3.11;

с = 0,125 – коэффициент, учитывающий влияние Mx  при изгибно-крутильной форме потери  устойчивости.

Коэффициент с следует определять:

– при значениях относительного эксцентриситета mх < 5 по формуле

c = b/(1 + amх),

где    a и b – коэффициенты, принимаемые по табл. 8.4;

– при значениях mх ³ 10 по формуле

c = 1/(1 + mхjy/jb),

где    jb в большинстве практических случаях при проверке устойчивости ко- лонны принимается равным 1,0 или определяется по СНиП как для балки

с двумя и более закреплениями сжатого пояса, для этого вычисляется коэффициент:

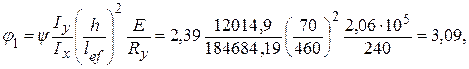
здесь lef – расчетная длина надкрановой части колонны, равная ly2, так как сжатая полка не закреплена связями по длине; значение y принимается по табл. 3.6 в зависимости от характера нагрузки и параметра a, который вычисляется для сварных двутавров, составленных из трех листов, по формуле

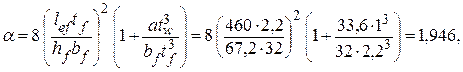
где    hf = hw + tf  = 65 + 2,2 = 67,2 см – расстояние между осями полок;

а – размер, равный 0,5hf  = 0,5 × 67,2 = 33,6 см.

Коэффициент y  = 2,25 + 0,07a = 2,25 + 0,07 × 1,946 = 2,39.

Таблица 8.4

Значения коэффициентов α и β

Обозначение: jс – значение jy приly = lc = 3,14

Значение коэффициента jb необходимо принимать: при j1 ≤ 0,85 –       jb = j1; при j1 > 0,85 – jb = 0,68 + 0,21j1, но не более 1,0. При j1 = 3,09 >     > 0,85 принимаем jb = 0,68 + 0,21 × 3,09 = 1,33.

При определении относительного эксцентриситета mх = (Mx/N2)/r за расчетный момент Mx принимается максимальный момент в пределах средней трети расчетной длины надкрановой части колонны (см. рис. 8.2):

М1/3 = М2,min + 2(M2,max – M2,min)/3 =

= 326,5 + 2 (1144,6 – 326,5) / 3 = 871,9 кН×м,

но не менее половины наибольшего по длине стержня момента:

Мх ³ М2,max/2 = 1144,6 / 2 = 572,3 кН×м.

Принимаем Мх = 871,9 кН×м.

Определяем:

mх = (Мх/N2)/r = (87190 / 479,3) / 25,64 = 7,09.

При значениях 5 < mх < 10 коэффициент с определяем по формуле

с = с5(2 – 0,2mх) + с10 (0,2mх – 1) =

= 0,12 (2 – 0,2 × 7,09) + 0,15 (0,2 × 7,09) = 0,125,

где    с5 = с = b/(1 + amх) = 1 / (1 + 1 × 7,09) = 0,12,

здесь a = 0,65 + 0,05mх = 0,65 + 0,05 × 7,09 = 1,0 при условии ly = 60,2 <

< 

с10 = с = 1 / (1 + mх jy /jb) = 1 / (1 + 7,09 × 0,8 / 1) = 0,15.

Проверка местной устойчивости элементов сплошной колонны

Местная устойчивость полки колонны обеспечивается за счет назначения соответствующего отношения расчетной ширины свеса bef (расстояние от грани стенки до края полки) к ее толщине tf.

Во внецентренно-сжатых элементах с условной гибкостью х от 0,8 до 4 отношение bef /tf  принимается не более значения, определяемого по формуле

bef /tf  = (0,36 + 0,1

При значениях х < 0,8 или х > 4 в формуле следует принимать соответственно х = 0,8 или х = 4.

Ширина свеса полки

 = (32 – 1) / 2 = 15,5 см.

Проверяем отношение при х = 2,14:

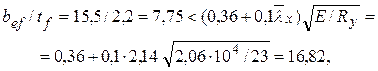
следовательно, устойчивость полки обеспечена.

Проверяем местную устойчивость стенки.

Для внецентренно-сжатых элементов двутаврового сечения отношение расчетной высоты стенки hef  = hw к толщине tw (гибкость стенки) определяется в зависимости от значения коэффициента a = (s – s1)/s, характеризующего распределение напряжений по сечению, где s – наибольшее сжимающее напряжение у расчетной границы стенки, принимаемое со знаком «плюс», и s1 – соответствующее напряжение у противоположной расчетной границы стенки.

Определяем (при yc = yp = hw/2 = 65 / 2 = 32,5 см):

s = N2/A + Mxyc/Ix = 479,3 / 205,8 + 114460 × 32,5 / 184684,19 = 22,47 кН/см2;

s1 = N2/A – Mxyр/Ix = 479,3 / 205,8 – 114460 ×32,5 / 184684,19 = – 17,81 кН/см2;

a = / 22,47 = 1,79.

При a £ 0,5 отношение hef/tw не должно превышать значений , где значения `luw определяются по табл. 4.2.

При относительном эксцентриситете mx = 9,32 > 1 и условной гибкости х = 2,14 > 2,0 предельная гибкость стенки определяется по формуле

hef /tw = 1,2 + 0,35= 1,2 + 0,35 × 2,14

При a ³ 1 предельная гибкость стенки вычисляем по формуле

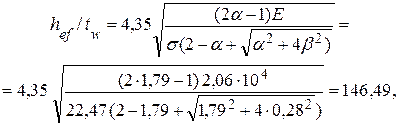
но не более 3,8= 3,8 = 111,34,

где    b = 1,4(2a – 1)t /s  = 1,4 × (2 × 1,79 – 1) 1,73 / 22,47 = 0,28,

здесь t = Q/(twhw) = 112,6 / (1 × 65) = 1,73 кН/см2 – среднее касательное напряжение в рассматриваемом сечении.

При 0,5 < a < 1 предельная гибкость определяется линейной интерполяцией между значениями, вычисленными при a  = 1 и a  = 0,5.

Сравниваем (при a = 1,79 > 1):

hef /tw = 65 / 1 = 65 < 111,34.

Стенка отвечает требованиям устойчивости.

В случае недостаточной жесткости стенки (hef/tw превышает критическое значение) увеличивают толщину стенки tw или стенка укрепляется парным или односторонним  ребрами  жесткости  с  моментом  инерции  ребра Isl ³ 6hef tw3 , расположенным посредине стенки. Наиболее нагруженную часть стенки между полкой и осью ребра рассматривают как самостоятельную пластинку и производят соответствующую проверку.

При расположении ребра с одной стороны его момент инерции вычисляется относительно оси, совмещенной с ближайшей гранью стенки.

Продольные ребра жесткости следует включать  в расчетное сечение колонны.

Минимальные размеры выступающей части продольных ребер жесткости bh принимаются:

– для парного симметричного ребра не менее hef /30 + 40 мм;

– для одностороннего ребра не менее hef  /24 + 50 мм.

Толщина ребра ts принимается из условия его устойчивости не менее 2bh.

Укрепление стенки продольными ребрами жесткости целесообразно при большой высоте сечения колонны (свыше 1000 мм).

В случаях, когда фактическое значение hef/tw превышает предельные значения, допускается использование закритической работы стенки, так как переход стенки в критическое состояние еще не означает потерю устойчивости стержня. В этом случае неустойчивая часть стенки выключается из работы и в расчетное сечение колонны при расчетах на устойчивость вместо площади А следует принимать значение A′. В состав рабочего сечения стенки включается два крайних устойчивых ее участка, непосредственно примыкающие к полкам шириной с = 0,65tw (рис. 8.4).

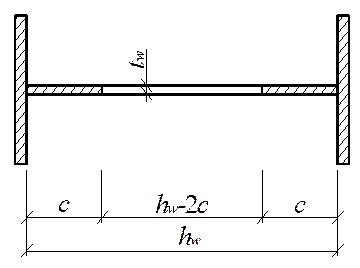
Рис. 8.4. Расчетное сечение колонны

Для двутаврового сечения при внецентренном сжатии

A′ = А – (hw – 2с) tw.

Исключение части стенки из расчетного сечения учитывается только при определении площади A′; все прочие геометрические характеристики определяются для целого сечения.

Стенку колонны при hef/tw ³ 2,3следует укреплять поперечными ребрами жесткости, расположенными на расстоянии (2,5 – 3)hef  одно от другого; на каждом отправном элементе должно быть не менее двух ребер.

Сварные швы, соединяющие стенку с полками, назначаются непрерывными с минимальным катетом шва и принимаются в зависимости от толщины наиболее толстого свариваемого элемента для уменьшения влияния возможных непроваров по табл. 3.5.