Проверка прочности и устойчивости балки

Проверка прочности балки. Вычисляем геометрические характеристики сечения балки:

– момент инерции сечения брутто

Ix = twhw3/12 + 2Af (hf /2)2 = 1,4 ∙1463 / 12 + 2 ∙ 100 ∙ (148 / 2)2 =

= 1458282,5 см4;

– момент инерции сечения нетто

Ix,n = twhw3/12 + 2Af,n(hf /2)2 = 1,4 · 1463 / 12 + 2 ∙ 90,8 ∙ (148/ 2)2 =

= 1357524,1 см4;

– момент сопротивления нетто верхнего пояса

Wx,А = 2Ix,n/h = 2 ∙ 1357524,1 / 150 = 18100,3 см3;

– момент сопротивления брутто нижнего пояса

Wx, н = 2Ix/h = 2 ∙ 1458282,5 / 150 = 19443,8 см3;

– статический момент полусечения относительно оси x-x

Sx = Af hf /2 + twhw2/8 = 100 ∙ 148 / 2 + 1,4 ∙ 1482 / 8 = 11130,3 см3.

Геометрические характеристики тормозной балки относительно вертикальной оси y-y:

– расстояние от оси подкрановой балки y0-y0 до центра тяжести

z = (Aшyш + Aлyл)/(Aш + Aл + Af,n) =

= (40,5 ∙ 122,45 + 63 ∙ 70,5) / (40,5 + 63 + 90,8) = 48,6 см;

– момент инерции тормозной балки

Iy = 327 + 40,5 ∙ 73,852 + 0,6 ∙ 1052 / 12 + 63 ∙ 21,92 + 2∙453 / 12 +

+ 90,8 ∙ 48,62 = 538,957 см4;

– момент сопротивления тормозной балки для крайней точки верхнего пояса

Wy,А = Iy/(48,6 + 22,5) = 5380,57 / 71,1 = 7580,3 см3.

Проверяем прочность балки:

– по нормальным напряжениям в верхнем поясе (точка А):

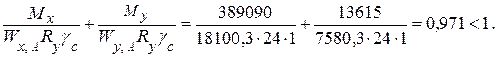
Недонапряжение в балке составляет

что допустимо в составном сечении согласно СНиП .

– по нормальным напряжениям в нижнем поясе:

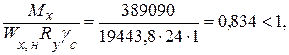
– по касательным напряжениям на опоре:

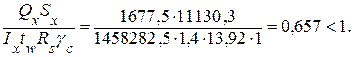
Проверяем прочность стенки балки при местном давлении колеса крана. Учитывая действия подвижной сосредоточенной нагрузки, передающей давление на стенку через верхний пояс в местах, не укрепленных ребрами жесткости, стенка подвергается местному давлению (рис. 9.4), что может привести к ее смятию:

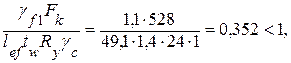
где    Fk – расчетная сосредоточенная нагрузка от колеса без учета коэффициента динамичности;

γf1 – коэффициент увеличения нагрузки на колесе, учитывающий возможное перераспределение усилий между колесами и динамический характер нагрузок, принимаемый равным:

1,6 – при кранах режима работы 8К с жестким подвесом груза,

1,4 – при кранах режима работы 8К с гибким подвесом груза,

1,3 – при кранах режима работы 7К,

1,1 – при прочих кранах;

lef – условная расчетная длина распределения сосредоточенной нагрузки Fk , зависящая от жесткости пояса с рельсом и сопряжения пояса со стенкой:

здесь с – коэффициент, учитывающий степень податливости сопряжения пояса и стенки: для сварных балок с = 3,25, для клепанных с = 3,75;

I1f – сумма собственных моментов инерции пояса и кранового рельса:

I1f = If + Ix,р = 50 ∙ 23 / 12 + 4794,22 = 4827,6 см4,

где    Ix,р = 4794,22 см4 – момент инерции подкранового рельса КР-120, принятый по табл. 9.2.

В случае приварки рельса швами, обеспечивающими совместную работу рельса и пояса, за I1f  принимают их общий момент инерции.

Проверяем стенку сварной балки на совместные действия всех напряжений на уровне верхних поясных швов по формуле

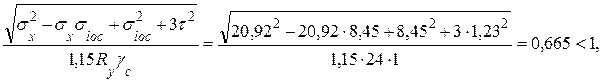
где    σx = (Мx/Wx,А)hw /hб = (389090 / 18100,3) 146 / 150 = 20,92 кН/см2;

τ = QMSf /(Ix,ntw) = 347,72 ∙ 6719,2 / (1357524,1 ∙ 1,4) = 1,23 кН/см2 –

касательные напряжения в сечении с максимальным изгибающим моментом Мх, здесь Sf  = Af,n(hf /2) = 90,8 (148 / 2) = 6719,2 см3 – статический момент пояса относительно оси х-х.

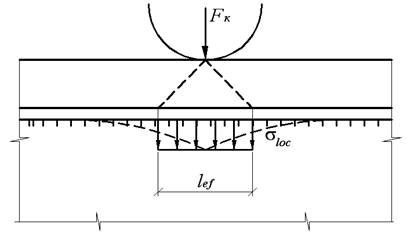
Рис. 9.4. Местные напряжения в стенке подкрановой балки

под колесом крана

Таблица 9.2

Характеристики подкранового рельса по ГОСТ 4121-76*

Прочность стенки балки от воздействия местного крутящего момента Мкр (рис. 9.5) проверяем по формуле:

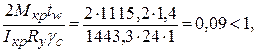
где

Mkp = Fkn2 γf γf1 e + 0,75Tkn γf hp = 480 ∙ 1,1 ∙ 1,1 ∙ 1,5 +

+ 0,75 ∙ 17,4 ∙ 1,1 ∙ 17 = 1115,2 кН∙см,

здесь е = 15 мм – условный эксцентриситет рельса, равный допустимому смещению рельса относительно оси подкрановой балки;

hp = 170 мм – высота подкранового рельса КР-120;

Iкр = It + Ikp,f  = 1310 + 133,3 = 1443,3 см4;

It = 1310 см4 – момент кручения рельса, принимается по табл. 9.2;

Iкр,f = bf tf3/3 = 50 ∙ 23 / 3 = 133,3 см4 – момент инерции кручения пояса.

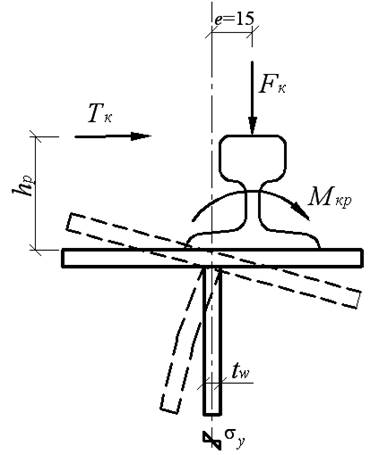
Рис. 9.5. Кручение верхнего пояса балки и изгиб стенки

Проверка общей устойчивости подкрановой балки не требуется, так как ее верхний сжатый пояс закреплен по всей длине тормозной конструкцией.

Местная устойчивость элементов подкрановой балки проверяется так же, как и обычных балок (см. п. 3.6.6).

Устойчивость поясного листа обеспечена отношением свеса сжатого пояса bef  к его толщине tf .

Определяем условную гибкость стенки:

Стенку балки следует укреплять поперечными ребрами жесткости, если значение условной гибкости при действии местной нагрузки превышает  Следовательно, постановка поперечных ребер жесткости необходима.

Ребра жесткости, обеспечивающие местную устойчивость стенки, в подкрановых балках должны иметь ширину не менее 90 мм. Торцы ребер следует плотно пригнать к верхнему поясу без приварки, при этом в балках под краны особого режима работы (7К и 8К) торцы ребер необходимо строгать.

Расстояние между ребрами жесткости а = 2hw = 2 ∙ 1460 = 2920 мм, принимаем а = 3 м.

Ширина выступающей части парного ребра

bp = hw/30 + 40 = 1460 / 30 + 40 = 88,7 мм ≈ 90 мм.

Толщина ребра

Принимаем ребра жесткости из полосовой стали по ГОСТ 103-76* сечением 90×7 мм (см. табл. 3.7). Ребра жесткости привариваются к стенке непрерывными угловыми швами минимальной толщины.

При наличии местного напряжения устойчивость стенки следует проверять, если условная гибкость .

Расчет на устойчивость стенки балки симметричного сечения, укрепленной только поперечными основными ребрами жесткости, при наличии местного напряжения смятия (σloc ≠ 0) и условной гибкости стенки  выполняется по формуле

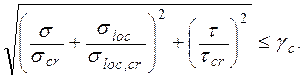
При наличии местных напряжений проверку стенки на местную устойчивость следует выполнять в зависимости от значения a/hw, при этом значения M и Q определяют в одном сечении балки.

Проверка местной устойчивости стенки при наличии местных напряжений в среднем отсеке (рис. 9.6). Так как а = 3 м > hw = 1,46 м, определяем средние значения Mср и Qср для наиболее напряженного участка с длиной, равной высоте отсека (стенки hw).

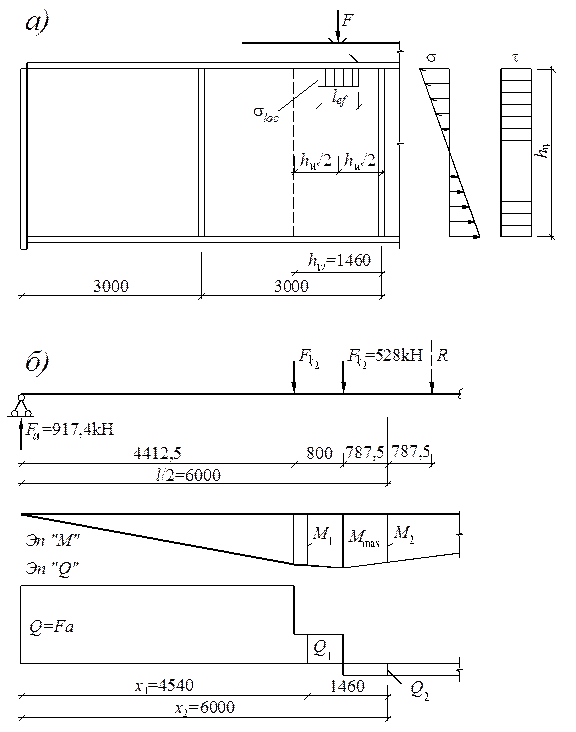
Рис. 9.6. К проверке местной устойчивости стенки балки в среднем отсеке:

 а – распределение напряжений в стенке; б – схема загружения балки и

эпюры М и Q

Вычисляем величины моментов и поперечных сил на границах расчетного участка (х1 = 4,54 м; х2 = 6 м):

Краевое напряжение сжатия в стенке составляет:

Среднее касательное напряжение  в отсеке равно:

Локальное напряжение σloc = 8,45 кН/см2.

При отношении a/hw =300/146 = 2,05 > 0,8 рассматривают два случая проверки устойчивости стенки:

Первая проверка.

Определяем значение критического нормального напряжения:

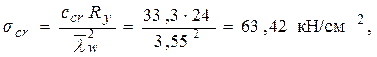
где    ccr = 33,3, коэффициент, определяемый в зависимости от значения коэффициента δ, учитывающего степень упругого защемления стенки в поясах (см. табл. 3.13):

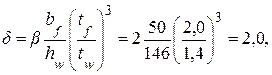
где    β – коэффициент, принимаемый для подкрановых балок, к которым не приварены крановые рельсы, равным 2.

Значение критического локального напряжения

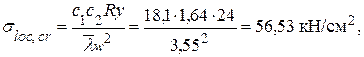
где при вычислении коэффициентов с1 и с2 при a/hw = 2 > 1,33 вместо а принимаем а1 = 0,67hw = 0,67 · 146 = 97,82 см, следовательно,

a1/hw = 97,82 / 146 = 0,67;

ρ = 1,04lef /hw = 1,04 ∙ 49,1 / 146 = 0,35 (здесь lef  = 49,1 см – условная длина распределения сосредоточенной нагрузки от колеса);

с1 = 18,1 – коэффициент, определяемый в зависимости от a1/hw = 0,67 и ρ = 0,35(см. табл. 3.14);

с2 = 1,64 – коэффициент, определяемый в зависимости от a1/hw = 0,67 и δ = 2 (см. табл. 3.15).

Значение критического касательного напряжения τcr во всех случаях вычисляют по фактическим размерам отсека:

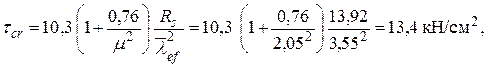
где    – отношение большей стороны отсека a или hw к меньшей d;

здесь d = hw = 1,46 м < a = 3 м.

Проверяем местную устойчивость стенки:

Вторая проверка. Значение критического нормального напряжения

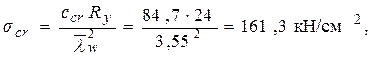
где    ccr = 84,7 – коэффициент, определяемый в зависимости от a/hw = 2,05 (см. табл. 3.16).

Значение критического локального напряжения

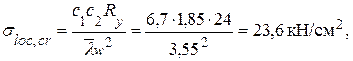
где    с1 = 6,7 – коэффициент, определяемый по табл. 3.14 в зависимости от     a1/hw = 2,05 и ρ = 0,35;

с2 = 1,85 – коэффициент, определяемый по табл. 3.15 в зависимости от   a/hw = 2,05 и δ = 2.

Значение критического касательного напряжения τcr = 13,4 кН/см2.

Проверяем местную устойчивость стенки:

Обе проверки показали, что стенка в среднем отсеке устойчива.

Аналогично поверяется устойчивость стенки в крайнем отсеке.

В балках большой высоты (h > 2 м) с тонкой стенкой при условной гибкости w > 5,5 для обеспечения ее устойчивости рационально, помимо поперечных ребер жесткости, ставить продольные ребра, опирающиеся на поперечные и располагаемые на расстоянии (0,2 – 0,3)hw от сжатой кромки отсека. Наличие продольного ребра разбивает стенку по высоте на верхнюю и нижнюю пластинки, устойчивость которых проверяется раздельно по СНиП .

Проверка прогиба подкрановой балки производится по правилам строительной механики. С достаточной точностью прогиб разрезной подкрановой балки определяется по формуле

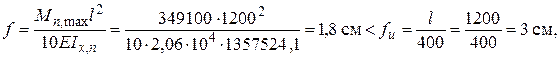
где    Mn,max – изгибающий момент в балке от нагрузки одного крана с γf  = 1;

fu – предельно допустимый прогиб подкрановой балки, устанавливаемый из условия обеспечения нормальной эксплуатации кранов в зависимости от режима их работы (fu = l/400 для режима работы 5К).

Жесткость балки обеспечена. Ее можно было не проверять, так как принятая высота балки hб > hmin.