Этот метод используется для показателей, представленных мультипликативными функциями. Рассмотрим его на примере двухфакторной модели П= а*x. Прологарифмируем её (по любому основанию):
![]() .
.
Если значение показателя изменяется с П0 до П1, то разность соответствующих логарифмов можно представить как
lg П1 - lg П0= (lga1- lga0)+(lgx1- lgx0)
или
lg П1/ П0 =lg(a1/a0)+ lg(x1/x0)
или ![]() .
.
Умножив на DП= П1- П0 правую и левую части последнего тождества получим:
![]() где Uп, Uа, Ux - индексы показателя и факторов.
где Uп, Uа, Ux - индексы показателя и факторов.
Здесь первое слагаемое в правой части определяет влияние фактора а на приращение показателя П, а второе - влияние фактора x.
Соответствующие модели могут быть разработаны для любого количества факторов.
Пример 1.6. С учетом данных примера 1.1. получим
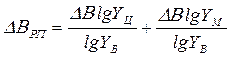 ;
;
DВРП=2500*11- 2400*12= -1300,
lgUв= lg0,955= -0,02,
lgUм= lg0,917= -0,0375,
lgUц= lg1,041= +0,0175,
-1300= (-1300)*(-0,0375)/(-0,02) +
((-1300)*0,0175)/ (-0,02) = -2438 + 1138.
Итак: общее изменение выручки DВРП= -1300 тыс.тг.,
в том числе: за счет изменения цены
DВРПц= +1138 тыс.тг.;
за счет изменения физического объема продукции DВРПм= -2438 тыс.тг.
Учитывая, что Uп=Uа*Ux формулу приращения показателя также можно представить в виде:
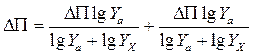 .
.
Поможем написать любую работу на аналогичную тему

