Новые методы обоснования рациональных решений

Новые методы широко применяются в планировании, особенно крупными компаниями. Они основаны на использовании экономико-математических моделей. Чтобы правильно применять эти методы в планировании, менеджеры, плановые работники должны знать области их использования и ограничения на различных этапах планирования при решении конкретных задач.

Для использования экономико-математических методов в планировании необходимо экономический объект или процесс записать с помощью математических зависимостей (уравнений, неравенств и т.п.). Этот процесс называется составлением модели.

Математическая модель - это система выражений, описывающих характеристики объекта моделирования и взаимосвязи между ними. Процесс моделирования заключается в построении моделей, которые облегчают изучение свойств планируемых процессов и объектов.

Моделирование является логико-математическим отображением структуры и процесса функционирования планируемого объекта с целью проведения на данной модели эксперимента. Сущность моделирования заключается в создании такого аналога изучаемых объектов, в котором отражены все их важнейшие с точки зрения цели исследования свойства и опущены второстепенные, малосущественные черты.

1. По форме представления модели могут подразделяться на следующие:

• графические, представляющие собой графическую имитацию

планируемого объекта или процесса;

• числовые, записанные в виде формул;

• логические, записанные в виде логических выражений, например блок-схем;

• табличные, записанные в виде таблиц, например бухгалтерский баланс.

2. С точки зрения отражения временных интервалов модели могут делиться на:

• динамические, отражающие свойства объекта планирования

изменять свои параметры во времени;

• статистические, не отражающие вышеуказанные свойства.

Во внутрифирменном планировании наиболее широкое применение нашли следующие экономико-математические методы:

• методы теории вероятности;

• методы математического программирования;

• методы имитации;

• методы теории графов.

Рассмотрим перечисленные методы.

/. Модели, основанные на использовании теории вероятности и математической статистики (стохастические модели)

К ним относятся модели, основанные на использовании теорий:

• анализа корреляций и регрессий;

• дисперсионного анализа;

• массового обслуживания;

• статистических испытаний;

• игр;

• статистических решений;

• информации;

• надежности;

• расписаний;

• запасов.

Методы теории анализа корреляций и регрессий, дисперсионного анализа применяются в планировании для анализа различных статистических связей и установления нормативов (трудовых, стоимостных, материальных).

Методы теории массового обслуживания используются при планировании оптимальных соотношений между размерами основного и вспомогательного производства, а также другими структурными элементами предприятия, если процессы в них носят нерегулярный характер и могут быть представлены как процесс массового обслуживания.

Методы теории игр и теории статистических решений применяются при принятии и оптимизации решений по управлению процессами взаимоотношения с рынком, страхованию от стихийных бедствий, созданию сезонных запасов ресурсов и т.д.

Применительно к планированию методы теории вероятности сводятся к определению значений вероятности наступления событий и действий и к выбору из возможных направлений действий самого предпочтительного, исходя из наибольшей величины математического ожидания (абсолютной величины этого исхода, умноженной на вероятность его наступления). Применение этих методов позволяет плановикам с большей уверенностью принимать решения на основе "приблизительных" оценок традиционными методами. Поэтому методы теории вероятности, как правило, применяются в комплексе с традиционными методами планирования, изложенными в § 3.2.

Например, методы теории вероятности хорошо применяются вместе с адаптивным поиском стратегии развития фирмы (см. п. 2, §3.2).

Адаптивное дерево поиска показывает возможные решения, подлежащие рассмотрению. По выбранным разветвлениям дерева возможным исходам приписывается та или иная вероятность. Результаты получают количественную оценку.

Ряд общих свойств деревьев решений можно проследить на рис. 3.4, где изображена ситуация, сложившаяся на текстильной фирме "Мартин текстайл милл" : вероятность возрастания в следующем году объема продаж на 20 % равна 0,6. Уровень продаж составляет 100 000 долл. Вероятность снижения уровня продаж на 10 % равна 0,4. Если сбыт увеличится, потребуется либо новое оборудование, либо сверхурочные работы. Комбинация этих двух вариантов возможна, но не рассматривается.

На дереве решений показаны: точка принятия решения, альтернативные варианты действий, случайные события, вероятности их свершения и чистый наличный доход. В нашем примере стоимость нового оборудования составляет 50 000 долл. Оплата сверхурочных работ потребует 10 000 долл. Таким образом, чистый денежный доход при больших объемах продаж будет равен 70 000 долл. (120 000 - 50 000) в случае закупки дополнительного оборудования, и 110 000 долл. - в случае введения сверхурочных работ (120 000 - 10 000).

Предполагается, что, если объем продаж снизится на 10 %, каких-либо сверхурочных работ не потребуется. Ясно, что при таких исходных данных компании гораздо выгоднее использовать сверхурочные работы и не закупать дополнительно оборудование.

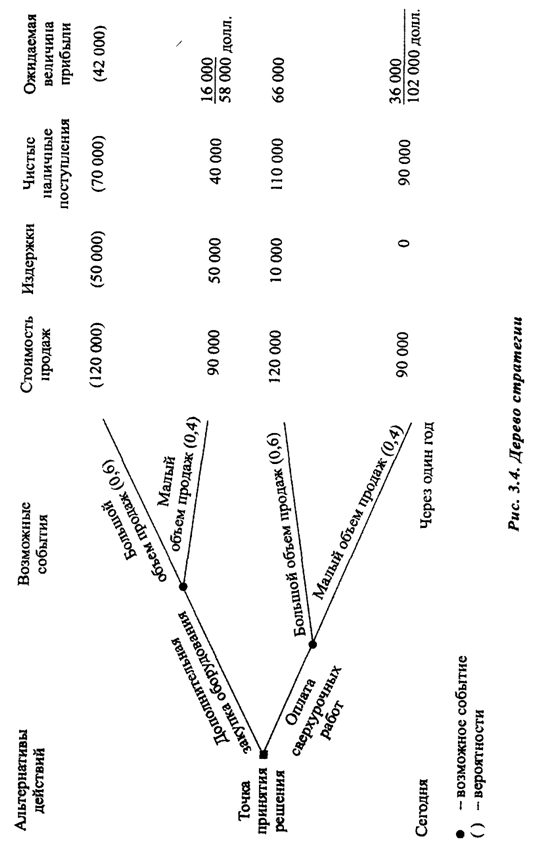
Такое решение основывается на сравнении денежных поступлений или суммарных величин стоимости событий, определенных исходя из вероятности их появления. Эта величина для случая закупки дополнительного оборудования подсчитывается путем умножения коэффициента вероятности 0,6 на ожидаемый объем и равна 0,6´70 000 = 42 000 долл. Тот же расчет продаж за вычетом амортизации для малых объемов продаж даст 16 000 долл. Сумма платежа будет равна 58 000 долларов.

Если компания изберет путь увеличения объемов производства за счет введения сверхурочных работ, то суммарный платеж (математическое ожидание) будет равен 102 000 долл. После вычета средств на оплату сверхурочных работ чистый денежный доход при больших объемах продаж составит 110 000 долл. Умножив эту величину на вероятность 0,6, получим 66 000 долл. При малых объемах продаж чистый денежный доход равен 90 000 долл., что дает 36 000 долл. Следовательно, суммарный платеж равен 102 000 долл. Введение сверхурочных работ предпочтительнее

Это решение - не единственно верное. Существует много причин, по которым руководство текстильной компании может принять решение закупить новое оборудование вместо применения сверхурочных работ, несмотря на то, что второй вариант сулит больший доход.

2. Методы математического программирования Они позволяют выбрать совокупность чисел, являющихся переменными в уравнениях и обеспечивающих экстремум некоторой функции при ограничениях, определяемых условиями работы планируемого объекта.

В зависимости от свойств функций, используемых в моделях математического программирования, модели разделяются на следующие классы:

а) модели линейного программирования, в которых применяются линейные зависимости между планируемыми параметрами,

б) модели нелинейного программирования, в которых некоторые функции нелинейны;

в) модели целочисленного программирования, в которых переменные в уравнениях по своему физическому смыслу могут принимать лишь ограниченное число дискретных значений;

г) модели параметрического программирования, если исходные параметры при переменных в моделях могут изменяться в некоторых пределах;

д) модели стохастического программирования, если с их помощью решаются в процессе планирования задачи экстремума при наличии случайных параметров в их условиях;

е) модели динамического программирования, позволяющие находить оптимальные решения по конечным результатам предыдущих решений;

ж) модели блочного программирования, которые в процессе планирования позволяют точно или приблизительно получать оптимальные решения задач больших размеров по решениям ряда задач с меньшим числом переменных ограничений.

Наиболее часто в процессах внутрифирменного планирования применяются задачи линейного программирования. Приведем в качестве примера некоторые задачи, которые могут быть решены с помощью данного метода.

Предприятие выпускает две модели бытовых холодильников. Первая модель - холодильник высокого класса, вторая — упрощенный вариант, в котором холодильная и морозильная камеры совмещены, предназначенный для продажи по низким ценам, но в больших количествах. Спрос на обе модели превышает предложение, но производственные мощности ограничены. При составлении плана производства возникает вопрос: сколько необходимо производить холодильников двух моделей, чтобы иметь максимальную прибыль?

При планировании поставок продукции часто возникает следующая задача. Необходимо переместить ряд товарных вагонов из одного места в другое с минимальными затратами. При относительно небольшом числе пунктов отправления и назначения и ограниченном количестве вагонов общее число возможных вариантов перевозок составит миллионы, что традиционными методами решить невозможно. Задачи такого класса встают перед крупными фирмами, когда требуется отгрузить различную продукцию многих заводов на многочисленные склады.

При составлении оптимального плана производства крупной горнодобывающей компании на 25 лет, необходимо учесть спрос, возможные изменения в технике, в геологических условиях и ряд других факторов, имеющих отношение к проблеме. Эта задача также может быть решена методом линейного программирования.

Несмотря на свою привлекательность, модели линейного программирования имеют серьезные недостатки. Основной из них заключается в том, что все зависимости в модели рассматриваются как линейные. Это значит, что, если затраты на перевозку одной тонны груза на один километр составляют 10 тыс. р., то при перевозке на 100 км они будут считаться равными 1 млн. Для большинства экономических задач зависимости носят нелинейный характер. Но во многих планируемых ситуациях в пределах интересующего нас лага зависимости можно считать линейными.

Другой недостаток линейного программирования состоит в том, что с его помощью можно решать только те задачи, для которых:

• существуют количественные цели, например максимизация

прибыли или минимизация издержек;

• распределяемые ресурсы имеют верхний предел, как, например, производственные мощности;

• варианты использования ресурсов могут сравниваться;

• имеется общая единица измерения;

• объем расчетов является выполненным.

И, наконец, большое число плановых задач насчитывает такое количество переменных, что решить задачу методами линейного программирования становится невозможным. В этом случае приходится упрощать задачу, что выдвигает вопрос, не приведет ли подобное упрощение к тому, что решение окажется бесполезным.

3. Методы имитации

Имитация представляет собой гибкий и продуктивный метод решения задач, получивший распространение на всех уровнях планирования - от стратегического до оперативно-календарного планирования.

В обычном смысле имитация означает воспроизведение реальной действительности. В планировании под имитацией понимают создание модели реальной хозяйственной ситуации и манипулирование с этой моделью в целях обоснования планового решения. Применение имитации в планировании не является чем-то принципиально новым. Словесные описания, таблицы, схемы - все это широко применялось и ранее, до появления моделей.

Ценность имитационных моделей объясняется рядом причин. Во-первых, экспериментирование в реальных условиях очень дорого, а порой просто невозможно. Во-вторых, для наблюдения за реальными изменениями, происходящими в экономике, требуется много времени. В-третьих, имитационные модели помогают плановым работникам лучше понять взаимосвязи факторов, действующих в экономике предприятия.

Имитационные модели широко применяются для решения следующих задач:

• распределения капитальных вложений в условиях возможного риска;

• составления смет капитальных затрат, направленных на максимизацию прибыли предприятия;

• планирования и контроля операций производственного цикла

• составления графиков движения транспорта;

• управления запасами;

• разработки политики кредитования банка путем моделирования использования займа различными клиентами;

• установления зависимости между производством, запасами и сбытом готовой продукции;

• планирования найма и подготовки кадров и т.д.

Как правило, имитационные модели применяются для определения:

• характеристик тех или иных систем, например системы управления запасами или финансами;

• сравнения различных систем (например, производства и снабжения);

• изучения последствий планируемых изменений внутри конкретной системы, например направление финансовых ресурсов по различным каналам.

Методы имитации имеют определенные ограничения:

• во-первых, сложности с созданием модели, написанием программы на ЭВМ и правильным применением модели требуют больших затрат времени и квалифицированного персонала, что не всегда имеется в распоряжении предприятия;

• во-вторых, существует опасность неадекватности установленной связи между некоторыми параметрами модели и реальной ситуации. В реальных условиях выявленная связь может не повториться или носить другой характер.

Имитация - достаточно сложный процесс, который зависит от специфики моделируемого объекта. Например, имитация возможных результатов капитальных вложений в процессе их планирования включает следующие этапы:

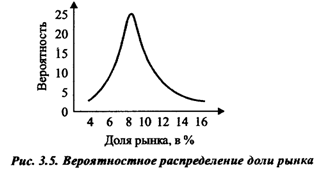
1. Построение кривых вероятностного распределения для всех параметров, участвующих в обосновании планового решения, например, размера и доли рынка; цены, затрат, связанных с исследованием рынка; издержек обращения; постоянных и переменных издержек производства; капиталовложений.

На рис. 3.5 приведена кривая вероятностного распределения доли рынка.

2. Имитация реальной ситуации на ЭВМ. ЭВМ выбирает по одному значению каждой переменной в соответствии с вероятностями их достижения.

3. На основе выбранных значений переменных рассчитываются нормы прибыли на вложенный капитал (НВК).

4. Выдача результатов и анализ полученных данных (по форме табл. 3.1).

Из табл. 3.1 видно, какой процент ситуаций приходится на тот или иной интервал значений нормы прибыли на вложенный капитал.

Таблица 3.1

Результаты имитирования реальной ситуации капитальных вложений

5. Построение кривой риска на основе кумулятивной величины вероятностей (рис. 3.6).

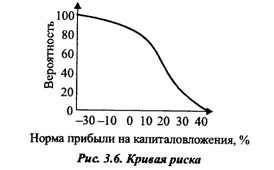
Из рис. 3.6 и табл. 3.1 видно, например, что вероятность получения прибыли на планируемые капитальные вложения составляет 78 %, а вероятность того, что они окажутся убыточными, равна 22 %. Имеется 5 шансов из 100, что норма прибыли составит 30-40 %.

Если руководство фирмы считает, что вероятность убытков слишком велика, можно получить иные вероятностные распределения, имитируя изменение ситуации различными действиями. Например, в нашем случае мы получим другой вид зависимости, если изменим соотношение объемов выпуска различной продукции, или проведем реконструкцию завода, или изменим стратегию сбыта или цены. Имитирующая модель может быть затем проиграна снова для определения влияния подобных изменений. Прежде чем принимать оперативные решения, управляющие могут проанализировать риск, связанный с осуществлением различных вариантов политики в области капиталовложений.

Вершиной достижений имитационного моделирования можно считать модель Джея Форрестера, охватывающую большую часть производственно-хозяйственной деятельности предприятия и получившую название индустриальной динамики, являющейся одновременно и концепцией планирования, и моделью.

Вот как характеризует свой метод сам Форрестер. Индустриальная динамика представляет собой изучение деятельности предприятия как системы с обратной связью, с тем чтобы показать, как влияют на успешную работу предприятия организационная структура, опережение и запаздывание. Она рассматривает взаимодействия между потоками денежных средств, заказов, материалов, рабочей силы и оборудования, связанными воедино через информационную сеть

Форрестер в своей модели рассматривает фирму как электрическую схему и определяет информационную структуру предприятия, факторы, вызывающие запаздывание, величину запаздывания в каждом структурном звене, а также политику и прогнозы, которые ведут к усилению возмущающего воздействия. Модель определяет последовательные связи между этими факторами и описывает их через математические уравнения. Поскольку число уравнений велико, потребовалось создать специальный язык, позволяющий перейти от системы уравнений к написанию рабочих программ ЭВМ. Такой язык был разработан и получил название "динамо".

Подобная модель позволяет управляющим в ситуации, представленной графиком на рис. 3.7, достичь гораздо большей стабильности (рис. 3.8) в работе. Оба рисунка представляют в весьма упрощенном виде довольно сложные графики, построенные с помощью ЭВМ на основании динамической модели программного предприятия.

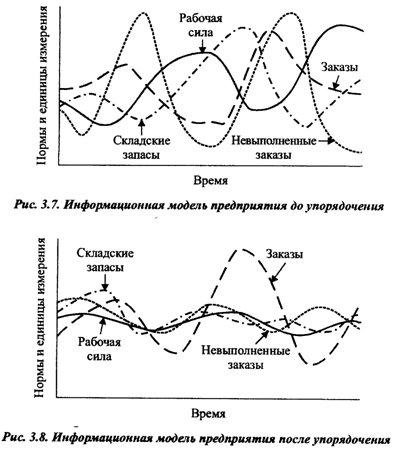
Модель позволяет сформулировать политику, дающую возможность улучшить взаимосвязи между переменными и соответствующим образом осуществлять планирование и контроль.

Широкое распространение в планировании получил метод Монте-Карло, особенно при анализе риска. Этот метод имитации применим для решения почти всех задач при условии, что альтернативы могут быть выражены количественно. Построение модели начинается с определения функциональных зависимостей в реальной системе, которые впоследствии позволяют получить количественное решение, используя теорию вероятности и таблицы случайных чисел.

Модель Монте-Карло не столь формализована и является более гибкой, чем другие имитирующие модели. Причины здесь следующие:

1) при моделировании по методу Монте-Карло нет необходимости определять, что именно оптимизируется;

2) нет необходимости упрощать реальность для облегчения решения, поскольку применение ЭВМ позволяет реализовать модели сложных систем;

3) в программе для ЭВМ можно предусмотреть опережения во времени.

Типичным примером задачи, которая может быть решена на основе модели Монте-Карло, может быть задача на обслуживание. Например, при планировании стратегии развития ресторана быстрого обслуживания необходимо знать, как долго в среднем приходится посетителю ждать обслуживания (среднее значение ожидания). Работа ресторана характеризуется следующими параметрами. Посетители обслуживаются последовательно на одной кухне. Прибытие клиентов носит случайный характер. Поступление заказов характеризуется следующими данными: интервалы поступления требований до 10 мин составляет 40 %, случаев от 10 до 20 мин. - 60 %. Продолжительность обслуживания в зависимости от вкусов клиентов - также величина случайная. В 80 % случаев на обслуживание требуется 10 мин., в остальных случаях-30 мин.

В табл. 3.2. представлены результаты решения задачи на основе имитационной модели Монте-Карло, в которой интервалы между прибытием клиентов и временем обслуживания представлены последовательностью случайных чисел.

Для интервалов между прибытиями выберем следующую случайную последовательность: 0, 1,2, 3, 4, 5, 6, 7, 8 или 9.

Если выбраны числа 0,1,2 или 3, то продолжительность интервала между поступлением двух требований составляет 10 мин. Если выбраны числа 4,5,6,7,8 или 9, продолжительность интервала равна 20 мин. Аналогичным образом определяется время обслуживания, которое наступает после истечения интервала прибытия. Для этого выбирается второе случайное число. Если выбраны числа 0,1,2,3,4 5,6 или 7, время обслуживания составит 10 мин. Если выбраны числа 8 или 9, обслуживание клиента длится 30 мин.

Из табл. 3.2 видно, что для 10 испытаний, приведенных в таблице суммарное время ожидания составляет 60 мин., или в среднем по 6 мин. на клиента. Данный пример оставляет без ответа многие вопросы, и среди них вопрос о необходимом количестве испытаний, позволяющем с достаточной точностью определить время ожидания.

Таблица 3.2 Решение задачи обслуживания с применением метода Монте-Карло

Примечание.   Колонка 8 = колонка 5 + колонка 7,

 колонка 9 = колонка 5 - колонка 4,

 колонка 10 = колонка 5 - цифра в предшествующем ряду колонки 8.

4. Метод оценки и пересмотра планов (ПЕРТ) В процессе оптимизации плановых решений применяется класс моделей, основанный на математической теории графов. Частным видом таких моделей являются модели сетевого планирования.

В зависимости от точности определения продолжительности работ модели сетевого планирования разделяются на:

• детерминистические;

• стохастические.

Идея графического изображения взаимосвязей между работами не нова. Новыми являются метод оптимизации временных и стоимостных параметров, критический путь и обработка информации о ходе работ на ЭВМ. Сочетание нового со старым и привело к созданию ПЕРТ, который явился важным открытием в практике и науке планирования.

ПЕРТ служит - если им правильно пользуются - мощным инструментом совершенствования планирования и управления сложными комплексами работ, связанных условиями значительной неопределенности. Благодаря этому методу управляющие могут быстро определить узкие места в выполнении графиков и распределять соответствующим образом ресурсы в целях ликвидации отставания. Выходя за рамки организационных структурных подразделений, метод позволяет обозреть весь комплекс работ, предусмотренных в планах компании.

Система ПЕРТ может быть реализована в нескольких вариантах:

• ПЕРТ/время;

• ПЕРТ/затраты.

1. ПЕРТ/время. Этот метод планирования имеет четыре отличительные особенности: сетевой график, временные оценки, определение резервов времени и критического пути, принятие в случае необходимости оперативных мер по корректировке графика.

Сетевой график ПЕРТ показывает последовательность этапов, необходимых для достижения заранее поставленной цели. Сетевой график включает: события, работы и зависимости.

Оценки продолжительности работ в методе ПЕРТ/время принимаются исходя из планируемых ресурсов и нормативов их использования.

Обычно для каждой работы сетевого графика требуется от одной до трех временных оценок.

Первая оценка производится для критического пути. Как видно из рис. 3.9, имеется одиннадцать путей, ведущих из "исходного события" к событию "контракт на производство выдан". Критический путь представляет собой сумму времен 10,42,10,5,13, 5 и 8 и равен 93 единицам времени, что больше продолжительности любого другого пути. Следовательно, ожидаемый срок наступления конечного события есть 93 (Те = 93).

Вторая временная оценка - ожидаемый срок наступления (Те) любого события, подсчитывается аналогично. Например, к событию "начало испытаний" ведут пять путей продолжительностью: 26, 57, 57,60 и 67 единиц времени. Следовательно, те = 67.

Третья временная оценка состоит в нахождении самого позднего из "наиболее поздних сроков" (ТL при котором еще не задерживается выполнение всей программы. На рис. 3.9 (возможно, это просто совпадение) наиболее поздний срок окончания работ также равен 93.

Вот почему в нашем примере резерв времени наступления конечного события, который представляет собой разность между наиболее поздним сроком (ТL и ожидаемым сроком (Tе), равен 0. Для различных комплексов работ нулевой резерв времени - величина желательная, но во многих случаях недостигаемая.

2. ПЕРП/затраты. Этот метод представляет собой дальнейшее развитие метода ПЕРТ/время в направлении оптимизации сетевых графиков по стоимости. Для метода ПЕРТ/затраты характерны следующие основные этапы:

1. Структурный анализ работ по проекту.

2. Определение видов работ.

3. Построение сетевых графиков.

4. Установление зависимостей между продолжительностью работ и их стоимостью.

5. Периодическая корректировка сети и оценок.

6. Контроль за ходом работ.

7. Проведение при необходимости мероприятий, обеспечивающих выполнение работ по плану.

По методу ПЕРТ/затраты суммарные затраты разбиваются на более мелкие элементы, пока они не достигают таких размеров, при которых становится возможным их планирование и контроль. Эти элементы представляют собой стоимость отдельных видов работ (например изготовление крыла или фюзеляжа). Отдельным видам работ присваиваются стоимостные значения, что позволяет суммировать стоимость групп работ на всех уровнях структуры работ.

По различным источникам методов, близких к ПЕРТ, используется более 100 разновидностей. Тем не менее, все они обладают рядом общих характеристик. К ним можно отнести следующие особенности применения ПЕРТ:

• система заставляет тщательно планировать проекты, для которых она используется;

• ПЕРТ делает возможным моделирование и эксперимент;

• применение метода расширяет участие в планировании специалистов низшего звена;

• повышается эффективность контроля;

• метод применим для решения многих планов задач;

• для сложных сетей стоимость применения системы ПЕРТ весьма значительна, что является существенным ограничением в применении на небольших объектах;

• неточность оценок снижает эффективность метода;

• если время осуществления событий нельзя предвидеть (как, например, в научных исследованиях), система не может быть использована.

В заключение сделаем ряд выводов:

Во-первых, эти методы являются ценными инструментами в руках тех управляющих, которые знают, как ими пользоваться.

Во-вторых, плановым работникам нет необходимости детально разбираться в данных методах, но они должны понимать, как их можно использовать с пользой.

В-третьих, каждый метод имеет свои слабые и сильные стороны. Поэтому эффективность плановых решений во многом зависит от их комплексного применения, в котором решающая роль принадлежит традиционным методам.