Агрегатное состояние вещества и теплопроводность

Механизм переноса тепловой энергии в веществах, находящихся в различных агрегатных состояниях, неодинаков. В газах и жидкостях он осуществляется хаотически движущимися молекулами, образующими однородную среду, в твердых телах — за счет взаимодействия соседних атомов решетки.

Однако внутри каждого вида агрегатного состояния имеют место свои особенности переноса энергии, которые, в свою очередь, зависят от структуры и свойств конкретного вещества.

В газах механизм переноса энергии и величина теплопроводности λ во многом зависят от расстояния между молекулами, т.е. определяются длиной их пробега l. В разреженных газах, когда l сравнимо с расстоянием между стенками L, ограничивающими объем газа, молекулы чаще сталкиваются со стенками, чем между собой. В результате происходит не направленный перенос тепла, а лишь теплообмен между молекулами в газовой среде. Следовательно, не соблюдается закон Фурье.

Если имеет место условие L >> l >> d, где d — диаметр твердой cферической молекулы газа, то согласно кинетической теории газов для теплопроводности идеальных газов справедливо следующее выражение:

λ = 1/3 ρсv.ν.l;

где       ρ — плотность газа, моль/м3;

сv -  удельная теплоемкость газа при V=соnst, Дж/моль°С;

ν — средняя скорость движения молекул, м/с;

1 — средняя длина свободного пробега частиц, м.

Кроме того, в идеальных газах теплопроводность λ связана еще и с вязкостью η соотношением:

λ = 5/2 η. сv

В плотных (реальных) газах расстояние между молекулами сравнимо с размерами самих молекул, а кинетическая энергия движения молекул и потенциальная энергия межмолекулярного взаимодействия — величины одного и того же порядка. В связи с этим перенос энергии столкновениями происходит значительно интенсивнее, чем в разреженных газах, и теплопроводность значительно выше.

В реальных газах зависимость теплопроводности от температуры и давления очень сложна, хотя при их увеличении теплопроводность газов растет.

Теплопроводность λ газов зависит от молекулярной массы М и количества атомов в молекуле n. При прочих равных условиях между λ и М существует следующая зависимость:

λ = 1/M0,5

Поэтому некоторые хлористые соединения, например фреоны, плохо проводят тепло.

Увеличение количества атомов в молекуле повышает теплопроводность в среднем на 2% на каждый атом. По этой причине бутан (n = 14) значительно более теплопроводен, чем сернистый газ (n=3), при примерно равных значениях молекулярных масс.

В жидкостях межмолекулярное расстояние еще меньше, чем в реальных газах. Плотность жидкости высока, а молекулы, хотя и подвижны, но не так хаотичны, как в газах, и перенос тепловой энергии осуществляется практически между слоями жидкости. Скорость такого распространения близка скорости распространения звука в жидкой среде νзв, а теплопроводность жидкости  описывается уравнением:

λ =  ρ.сv. νзв.l;

Как видно из этого уравнения, теплопроводность жидкости λ тем больше, чем выше ее удельная теплоемкость сv и плотность ρ. При повышении температуры жидкости расстояние между молекулами увеличивается, жидкость расширяется, а ее теплопроводность снижается. Исключения составляют вода, тяжелая вода и глицерин.

Химический состав жидкости влияет на теплопроводность через изменение температуры кипения. Чем ниже температура кипения жидкости, тем выше скорость уменьшения ее теплопроводности при нагревании.

В твердых телах перенос тепловой энергии осуществляется с помощью двух основных механизмов:

- за счет взаимодействия между тепловыми упругими колебаниями решетки;

- за счет движения электронов и столкновения их с атомами.

В большинстве случаев теплопроводность твердых тел λ складывается из теплопроводности решетки λреш и теплопроводности электронами λэл т.е. условно λ = λреш + λэл.

В неорганических, неметаллических, тугоплавких материалах (керамика, природные каменные материалы, бетоны и др.) количество свободных электронов, которые могли бы двигаться через кристаллическую решетку и осуществлять перенос энергии, недостаточно и теплота в основном передается за счет колебаний решетки.

Величина теплопроводности зависит от характера колебаний решетки. При гармонических колебаниях сопротивление переносу энергии отсутствует и теплопроводность может достигать огромных значений. Однако в реальных кристаллах колебания имеют ангармонический характер, который способствует частичному затуханию упругих тепловых колебаний и значительному снижению теплопроводности.

В теории теплопроводности предполагается, что колебания нормального вида квантуются и по аналогии с фотонами в теории света эти кванты называют фононами, а механизм переноса тепловой энергии — фононной теплопроводностью.

Таким образом, у твердых неметаллических тел перенос тепловой энергии осуществляется за счет взаимодействия фононов, в результате их движения, сталкивания, рассеивания и т.п. По аналогии с кинетической теорией газов фононную теплопроводность твердых тел можно представить как

λ = с ν l;

где l – длина свободного пробега фононов.

с — удельная теплоемкость тела;

 ν — средняя скорость фононов;

В металлах перенос тепловой энергии определяется движением и взаимодействием электронов проводимости, так как решетчатая фононная составляющая теплопроводности исчезающе мала и λэл>> λреш.

Явление переноса тепла в полупроводниках сложнее, чем в диэлектриках и металлах, так как для них существенны как решеточная, так и электронная составляющие теплопроводности. Кроме того, здесь теплопроводность зависит от теплопроводности примесей и многих других факторов.

Влияние состава, структуры и параметров состояния на фононную теплопроводность твердого тела (кристалла)

Анализируя механизм переноса тепловой энергии в неорганических, неметаллических материалах (кристаллах), заметим, что основными факторами, влияющими на величину теплопроводности, являются:

- теплоемкость

- средняя скорость движения частиц (фононов);

- средняя длина свободного пробега частиц (фононов);

- степень гармоничности (ангармоничности) колебания решетки.

По изменениям этих параметров можно объяснить закономерности влияния состава, структуры, температуры и давления на теплопроводность того или иного тела.

Рассмотрим влияние структуры на теплопроводность кристаллов. Напомним, что структура кристаллов определяется типом химических связей и строением кристаллической решетки. Состав и структура кристаллов тесно взаимосвязаны, поэтому и оказывают совместное влияние на теплопроводность.

Известно, что строение кристаллической решетки и характер ее колебания влияют на степень отклонения гармоничности колебаний.

Ангармоничность обусловливается прежде всего различием атомных масс ионов решетки. Это различие вызывает так называемое рассеяние колебания с уменьшением средней длины пробега частиц. В результате этого теплопроводность уменьшается. Так, у оксидов и карбидов с легкими катионами, атомная масса которых близка соответственно атомной массе кислорода и углерода, теплопроводность оказывается более высокой, чем у оксидов и карбидов с тяжелыми катионами.

Расположение атомов в решетке влияет на образование осей симметрии и, как следствие, на анизотропию кристаллов. Теплопроводность в отличие от теплоемкости является анизотропным свойством; для многих кристаллов ее величина λ почти в 2 раза больше при потоке тепла параллельно оси симметрии, а не перпендикулярно к ней.

У кристаллов с простым строением решетки термическое рассеяние мало, а l велико, поэтому их теплопроводность высокая.

Кристаллы с более сложным строением решетки в общем имеют большее рассеяние тепловых упругих волн, увеличивающее ангармоничность ее колебания и, следовательно, пониженную теплопроводность.

Введение второго компонента в основной кристалл (твердые растворы) вызывает:

- усложнение строения кристаллической решетки;

- образование дополнительных центров рассеяния и, как следствие, уменьшение средней длины свободного пробега частиц.

В результате совместного влияния этих факторов теплопроводность нового соединения оказывается значительно ниже теплопроводностей его составляющих. Например, глинозем (Аl2O3) и периклаз (МgO) имеют примерно равные, но очень высокие значения теплопроводности, порядка 30. . .35 Вт/м.К, в то время как теплопроводность алюмомагнезиальной шпинели (МgO.А12O3) значительно ниже — порядка 13...15 Вт/м.К. Другой пример: глинозем (А12О3) и кремнезем (SiO2) — простые компоненты, а муллит (3 А12О3. 2SiO2) — сложное соединение. В обоих случаях примесные компоненты МgO и SiO2 значительно уменьшают теплопроводность соединения за счет усложнения строения кристаллической решетки и уменьшения средней длины свободного пробега частиц.

Взаимосвязь температура и теплопроводность твердого тела сложна и неоднозначна. Она определяется характеристической “температурой Дебая” (температура Дебая – интервал от 100 до 1000о К), которая устанавливает для каждого вещества температурную границу, выше которой не улавливаются квантовые эффекты, и фононовая теплопроводность теряет физический смысл.

Для большинства обжиговых и плавленых материалов эта температурная граница находится в пределах 100... 1000 К. В таком интервале температур составляющие формулы фононной теплопроводности, удельной теплоемкости и скорости распространения фононов практически остаются неизменными, а средняя длина свободного пробега фононов, с учетом теории теплоемкости, должна быть обратно пропорциональной абсолютной температуре, хотя имеются многочисленные исключения.

Итак, с увеличением температуры кристалла средняя длина свободного пробега частиц сокращается, ангармоничность растет и теплопроводность, уменьшается.

При температурах выше 1500оС теплопроводность огнеупорных оксидов обычно увеличивается, так как составляющая переноса тепла излучением значительно превосходит фононную.

Влияние давления на теплопроводность твердых тел выражается линейной зависимостью. Для многих минералов и металлов теплопроводность растет с увеличением давления.

Теплопроводность некристаллических тел

Тела с сильно разупорядоченной кристаллической решеткой, а также с полностью некристаллическим строением имеют очень низкую среднюю длину свободного пробега фононов, которая находится в пределах межатомного расстояния (порядка 3.. .5 Ǻ). Этим в основном объясняется низкая теплопроводность стекол и других аморфных тел и ее слабая зависимость от температуры.

Данные по теплопроводности стекол, приведенные в табл. 4.3., являются типичными для некристаллических твердых тел. Как видно из таблицы, их теплопроводности очень близки, хотя состав стекла все же оказывает некоторое влияние. Например, стекла с высоким содержанием бария или свинца имеют теплопроводность ниже, чем натрий, калий, силикатные стекла.

Таблица 4.3. Теплопроводность различных твердых тел

Стекловидная фаза, которая обычно выполняет роль связки в традиционной керамике, имеет теплопроводность, близкую к теплопроводности натрий, калий, силикатного стекла.

Природные и синтетические полимеры ввиду особого строения макромолекул обладают самой низкой теплопроводностью из твердых веществ и соединений (см. табл. 4.3), потому что такие легкие элементы, как С, О, Н и др., образуют ковалентную связь, и можно предположить высокую теплопроводность их молекул. Однако из-за слабости и неоднородности молекулярных связей рассеяние фононов оказывается значительным, а теплопроводность низкой.

В зависимости от агрегатного состояния веществ и особенностей переноса ими тепловой энергии условный ряд тел по величине их теплопроводности (по мере возрастания) может иметь следующий вид:

газы <<полимеры<<жидкости<<стекла<<кристаллы<<металлы,

Существенное изменение теплопроводности тел при изменении их состава и температуры и проявление в различных интервалах температур разных механизмов переноса тепла усложняет анализ этого явления ввиду значимости каждого фактора и их взаимосвязей.

Следует заметить, что для каждого агрегатного состояния тела имеется параметр (критерий), определяющий интервал состояния тела, за пределами которого его свойства резко изменяются. Такими параметрами (критериями) являются:

- для газа — соотношение между суммарным объемом частиц и общим объемом, занимаемым газом, т.е. величина, которая определяет его плотность и, следовательно, теплопроводность;

- жидкости — температура кипения, определяющая скорость изменения теплопроводности при изменении температуры;

- кристаллических тел — температура Дебая, которая определяет эффективные параметры упругих колебаний кристаллической решетки, обеспечивающих перенос тепловой энергии.

Теплопроводность гетерогенных систем

В строительном материаловедении теплопроводность λ учитывается при расчете ограждающих конструкций для обеспечения:

- тепловой изоляции зданий и сооружений

- тепловой защиты поверхностей тепловых агрегатов и трубопроводов;

- термостойкости огнеупорных материалов и специальных составов;

- хладоизоляции.

Поскольку ограждающие конструкции по своему назначению многофункциональны, составляющие их материалы, как правило, являются гетерогенными пористыми телами. Общая, или эффективная теплопроводность таких систем определяется теплопроводностями твердых и газовых фаз:

λ = λтв +  λгаз

Однако, учитывая тот факт, что теплопроводность является векторной величиной, ее суммарное значение для гетерогенных систем зависит не только от количественного соотношения фаз, но и от их взаимного расположения, характера пограничного слоя, степени непрерывности или дискретности фаз и т.д., т.е. от структуры и текстуры материала.

Чтобы оценить эффективную теплопроводность системы, рассмотрим влияние каждой составляющей.

Для оценки зависимости теплопроводности системы от сочетания твердых фаз приведем в качестве примера три упрощенных варианта сочетания твердых фаз двухфазной системы:

- параллельное расположение слоев (фаз), свойственное слоистой структуре материалов (рис.4.4, а);

- основная фаза является непрерывной, а другая - в виде отдельных включений, что соответствует структуре стеклокристаллических материалов (рис.4.4. б);

- основная фаза является дискретной, соответствует структуре, подобной конгломератам, например бетонам, (рис.4.4. в).

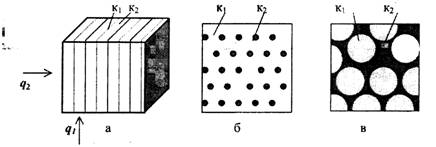
                    Рис. 4.4. Схемы распределения фаз:

а - параллельными слоями; б - с непрерывной основной фазой;

в - с дискретной основной фазой; к1 - основная фаза, к2 - вторая фаза;

q1, q2 - направления теплового потока

Вариант 1 Слоистая структура (см. рис. 4.4. а)

Если тепловой поток q направлен вдоль слоев, то λ рассчитывается так же, как и электропроводность цепи с параллельно включенными сопротивлениями. При одинаковом ΔТ во всех слоях большая часть тепла переносится через фазу с более высокой теплопроводностью. Среднюю теплопроводность можно рассчитать по формуле:

λср = V1 λ1 + V2 / λ2

где V1 и V2 — объемные доли каждой фазы.

В этом случае общая теплопроводность системы определяется в основном фазой с более высокой теплопроводностью, и если λ1 >> λ2, то  λср= V1 λ1.

Если тепловой поток направлен перпендикулярно к плоскости слоев, то имеет место случай, аналогичный случаю электрической цепи с последовательным включением сопротивлений. Тепловой поток, проходящий через все слои, остается величиной постоянной, тогда как ΔТ по слоям различна, и общая теплопроводность определяется соотношением:

1 /λср = V1/λ1 +V2/ λ2 или λср = λ1 λ2/( V1 λ1 + V2 λ2)

В этом случае общая теплопроводность определяется в основном фазой с меньшёй теплопроводностью, и если λ1 >> λ2, то λср~~ λ2/ V2.

Вариант 2. Структура с непрерывной основной фазой (см. рис.4.4. 6).

Если вторая фаза дискретна и по величине не превышает 10%, то общая (средняя) теплопроводность системы определяется теплопроводностью непрерывной фазы.

Вариант З.  Структура с дискретной основной фазой (см. рис.4.4. в).

Если содержание второй фазы превышает 10%, то главным фактором, определяющим теплопроводность системы, является соотношение фаз, и условно непрерывной фазой становится большая из них. Общую теплопроводность системы определяют исходя из соотношений Максвелла-Эйкена для непрерывной среды с λ1 и диспергированной в нее фазой с λ2:

Если λ1 >> λ2 , то λср = λ1(1- V2)/(1+ V2).

Если λ1<< λ2, то λср = λ2(1 + 2 V2)/(1 - V2).

Как влияет газовая фаза на теплопроводность системы? Выше упоминалось о том, что гетерогенные системы (неорганические, не металлические материалы), как правило, имеют значительную газовую составляющую, которая колеблется от доли процента у плотных природных каменных материалов до 99% у искусственных полимерных материалов.

Тот факт, что с увеличением газовой фазы или пористости теплопроводность системы уменьшается, не вызывает сомнения. Например, теплопроводность воздуха примерно в 20 раз меньше теплопроводности керамического черепка. Однако необходимо выделить два момента:

- при увеличении пористости теплопроводность системы уменьшается за счет сокращения объема более теплопроводной твердой фазы, что не требует доказательства;

- при увеличении пористости теплопроводность системы снижается еще и за счет уменьшения теплопроводности самой твердой фазы.

Такая закономерность объясняется тем, что поры, образуя новые поверхности в плотной структуре, становятся центрами рассеяния, примерно такими, как дефекты решетки, границы зерен примеси и пр. При этом уменьшается средняя длина свободного пробега частиц и снижается фононная теплопроводность системы.

Если пренебречь влиянием границ зерен и другими факторами, а также теплопроводностью самих пор (т.е. газовой составляющей) и допустить, что поры равномерно распределены в непрерывной среде, то можно получить уравнение Максвелла-Эйкена, показывающее влияние пористости на фононную теплопроводность гетерогенной системы:

λ = λср(1-П)(1+0,5П);

где λ, λср — соответственно теплопроводности системы и твердой фазы в абсолютно плотном состоянии;

П — пористость системы, ед.

Приведенное соотношение теплопроводность — пористость условию для непрерывной твердой фазы с изолированными порами. Однако если непрерывной является газовая фаза, как в порошкообразных и волокнистых материалах, то необходимо учитывать и ее теплопроводность, которая определяется конвективным теплопереносом а, а при температурах выше 600°С — еще и излучением  «кч».

При расчете эффективной теплопроводности с учетом конвекции и излучения определяющими факторами являются размер пор и температура. Так, влияние переноса теплоты излучением на теплопроводность пор пропорционально их условному диаметру d и кубу температуры, Следовательно, наличие крупных пор приводит к повышению общей теплопроводности системы, особенно при высокой темпера туре, в то время как мелкие поры являются хорошим препятствием для переноса теплоты.

Следует, однако, снова упомянуть о том, что на теплопроводность  влияет не только размер пор, но и непрерывность поровой среды. Причем влияние последнего фактора значительнее.

Из опыта применения высокотемпературной теплоизоляции известно, что в сыпучих и волокнистых материалах, где непрерывной средой является воздух, размер пор, а, следовательно, и размер зерен или толщина волокон практически не оказывают влияния на теплопроводность материалов при низких температурах.

При высоких температурах размер зерен становится значимым параметром, так как с увеличением конвективной составляющей теплопереноса резко возрастает фактор излучения. Поэтому для высокотемпературной изоляции наиболее эффективными являются мелкозернистые или мелкопористые материалы. Теплопроводность же самой твердой фазы или зерна в данном случае имеет второстепенное значение.

При высоких температурах размер зерен становится значимым параметром, так как с увеличением конвективной составляющей теплопереноса резко возрастает фактор излучения. Поэтому для высокотемпературной изоляции наиболее эффективными являются мелкозернистые или мелкопористые материалы. Теплопроводность же самой твердой фазы или зерна в данном случае имеет второстепенное значение.