Стороны и диагонали квадрата выражают возможные типы отношений между простыми суждениями. Истинная характеристика относится к суждениям имеющим один и тот же S и P.
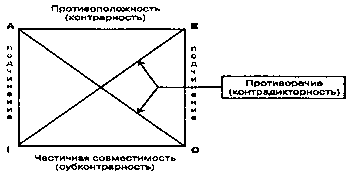
Отношения между A и E называются противоположными или контрарными. Отношения противоположности имеют место между общими суждениями. Отношения противоречия - по диагонали. Отношения подчинения по вертикалям. Отношения между J и O, подпротивности.
Отношения противоположности – суждения находящиеся в отношении противоположности не могут быть одновременно истинными, но могут быть одновременно ложными. Все мужчины галантны. Ни один мужчина не галантен. Если одно из противоположных истинно, то другое ложно, но не наоборот.
А истинно, Е ложно. ∀ (x)(S(x) ⊃ P(x)) ⊃ ∀- (x)(S(x) ⊃ P-(x)) Если верно, что все S суть P, то неверно, что ни одно S не суть P.
Отношения противоречия – суждения находящиеся в состоянии противоречия не могут быть одновременно не ложными, не истинными. Если одно из них истинно, то другое непременно ложно, и наоборот.
А истинно, O – ложно. ∀ (x)(S(x) ⊃ P(x)) ⊃ ∃- (x)(S(x) ⋀ P-(x)) Если верно, что все S суть P, то неверно, что некоторые S не суть P.
Отношения подчинения – суть отношений подчинения заключается в том, что истинность подчинённых суждений, гарантируется истинностью общих суждений.
Ложность подчинённых, обуславливает ложность общих.
A истинно, E – ложно. ∀ (x)(S(x) ⊃ P(x)) ⊃ ∃ (x)(S(x) ⋀ P(x)) Если верно, что все S суть P, то верно, что и некоторые S суть P.
Отношения подпротивности – суждения находящиеся в отношении подпротивности не могут быть одновременно ложными, но могут быть одновременно истинными. Если одно из суждений ложно, то другое непременно истинно, но не наоборот.
Поможем написать любую работу на аналогичную тему