Обозначим через r радиус сферической поверхности раздела фаз (радиус капли), через Р0 – давление насыщеного пара над плоской (r = ¥), а через Р – над выпуклой поверхностью. Перенесем некоторое количество жидкости dm с плоской поверхности жидкости в каплю радиуса r путем обратимого изотермического испарения при давлении Р0, обратимого сжатия пара от Р0 до Р и последующей обратимой изотермической конденсации при Р. Поскольку работа испарения и конденсации равны и противоположны по знаку, то общая работа переноса dW, совершаемая над системой, оказывается работой сжатия пара:
, (12.15)
где М – молярная масса вещества.
С другой стороны, в результате переноса dm вещества увеличивается масса капли за счет увеличения ее радиуса на dr и поверхность на dS, что требует затраты энергии на работу против сил поверхностного натяжения (работу увеличения поверхности).
В обоих случаях осуществляется перенос количества dm, поэтому работы dW1 и dW2 равны по абсолютной величине и противоположны по знаку:
. (12.16)
Так как m капли с радиусом r равна m = 4/3pr3r, где r - плотность жидкости - то dm = 4prr2dr. Поверхность капли S = 4pr2, поэтому dS = 8prdr. Подставим эти значения dm и dS в уравнение (12.16) и решим его относительно r. Получим:
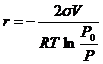(12.17)
(V – молярный объем жидкости 
), что являет собой уравнение Томсона для выпуклой поверхности.
Для вогнутой поверхности кривизна отрицательна. Поэтому:
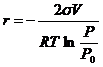. (12.18)
Уравнение Томсона (Кельвина) и уравнение Лапласа являются основными уравнениями физической химии поверхностных явлений.
Поможем написать любую работу на аналогичную тему