Капиллярная конденсация. Формула Жюрена.

Капилярную концетрацию найти не удалось, возможно это:

Равновесие твердых частиц по отношению к жидкому раствору можно выразить уравнением, сходным суравнением Томсона. В растворе мерой интенсивности перехода вещества в другую фазу является концентрация насыщенного раствора, и тогда применительно к дисперсной системе твердая фаза – раствор можно записать:

,                                                                                              (12.19)

где С0 – концентрация насыщенного раствора, С – концентрация вещества в растворе, равновесном с кристалликами размером r. Поэтому при растворении высокодисперсных веществ можно получить концентрацию раствора выше обычной растворимости.

Далее идёт повтор 4-того вопроса, но это точно формула Жюрена!

Капиллярные явления наблюдаются, когда жидкость проникает в трубки с очень узкими каналами (капилляры, капиллярно-пористые тела), у которых расстояние между стенками соизмеримо с радиусом кривизны поверхности жидкости. Кривизна возникает в результате взаимодействия жидкости со стенками сосуда (адгезия, смачивание). Специфика поведения жидкости в капилляре зависит от того, смачивает или не смачивает жидкость его стенки, точнее, от значения краевого угла смачивания.

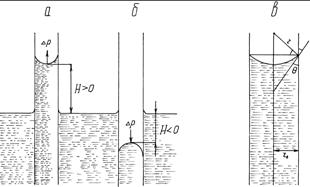
Рассмотрим положение уровней жидкости в двух капиллярах, один из которых имеет лиофильную поверхность и поэтому стенки его смачиваются, у другого внутренняя поверхность лиофобизирована и не смачивается (рис.30).

В первом капилляре (см. рис.30, а) поверхность жидкости имеет отрицательную кривизну, поэтому дополнительное давление Лапласа (давление направлено к центру кривизны) поднимает ее в капилляре. Кривизна поверхности жидкости во втором капилляре (см. рис.30, б) положительна, дополнительное давление направлено внутрь жидкости, в результате жидкость в капилляре опускается (отрицательное капиллярное поднятие). При равновесии лапласовское давление равно гидростатическому давлению столба жидкости высотой H:

                                (XII.3)

где  - плотность жидкости; 0 - плотность газовой фазы; g - ускорение свободного падения; r - радиус мениска.

Рис.30. Капиллярное поднятие жидкости:

a - cos q > 0: б - cos q < 0: в - связь радиуса кривизны мениска r с радиусом капилляра r0.

Чтобы высоту капиллярного поднятия связать с характеристикой смачивания, радиус мениска необходимо выразить через угол смачивания q и радиус капилляра r0. На рис.30, в показан (в увеличенном виде) мениск жидкости в капилляре. Видно, что r0 = r cosq , тогда высоту капиллярного поднятия можно представить в виде формулы Жюрена:

                                          (XII.4)

При отсутствии смачивания q > 90°, cos q < 0, уровень жидкости в капилляре опускается на величину H. При полном смачивании q = 0, cos q = 1, в этом случае радиус мениска равен радиусу капилляра.