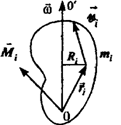
Рассмотрим твердое тело, которое может вращаться относительно некоторой оси (рис.). Момент импульса i-й точки тела относительно этой оси определяется формулой:
![]() . (1.84)
. (1.84)
Выражая линейную скорость точки через угловую скорость тела и используя свойства векторного произведения, получим
![]() (1.85)
(1.85)
Спроектируем момент импульса на ось вращения: — эта проекция определяет момент относительно этой оси. Получим
![]() . (1.86)
. (1.86)
где zi,- координата i—точки вдоль оси Z, a Ri, — расстояние точки от оси вращения. Суммируя по всем частицам тела, получим момент импульса всего тела относительно оси вращения:
![]() . (1.87)
. (1.87)
Величина
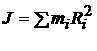 (1.88)
(1.88)
является моментом инерции тела относительно оси вращения. Момент импульса тела относительно данной оси вращения принимает, таким образом, вид:
Mz = J·ω. (1.89)
Полученная формула аналогична формуле Pz = mVz для поступательного движения. Роль массы играет момент инерции, роль линейной скорости — угловая скорость. Подставив выражение (1.89) в уравнение для момента импульса (2.74), получим
J·βz = Nz. (1.90)
где βz. — проекция на ось вращения углового ускорения ![]() . Это уравнение эквивалентно по форме второму закону Ньютона.
. Это уравнение эквивалентно по форме второму закону Ньютона.
В общем случае несимметричного тела вектор M не совпадает по направлению с осью вращения тела и поворачивается вокруг этой ocи вместе с телом, описывая конус. Из соображений симметрии ясно что для однородного тела, симметричного относительно оси вращения, момент импульса относительно точки, лежащей на оси вращения, совпадает с направлением оси вращения. В этом случае имеет место соотношение:
![]() . (1.91)
. (1.91)
Из выражения (1.90) следует, что при равенстве нулю момент внешних сил произведение Jω остается постоянным Jω = const и изменение момента инерции влечет за собой соответствующее изменение угловой скорости вращения тела. Этим объясняется известное явление, состоящее в том, что человек, стоящий на вертящейся скамье, разводя руки в стороны либо прижимая их к туловищу, изменяет частоту вращения.
Из полученных выше выражений ясно, что момент инерции является такой же характеристикой свойства инерции макроскопического тела в отношении вращательного движения, как инертная масса материальной точки в отношении поступательного движения. Из выражения (1.88) следует, что момент инерции вычисляется путем суммирования по всем частицам тела. В случае непрерывного распределения массы тела по его объему естественно перейти от суммирования к интегрированию, вводя плотность тела. Если тело однородно, то плотность определяется отношением массы к объему тела:
![]() . (1.92)
. (1.92)
Для тела с неравномерно распределенной массой плотность тела в некоторой точке определяется производной
![]() . (1.93)
. (1.93)
Момент инерции представим в виде:
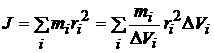 , (1.94)
, (1.94)
где DV — микроскопический объем, занимаемый точечной массой.
Поскольку твердое тело состоит из большого числа частиц, практически непрерывно заполняющих весь занимаемый телом объем, в выражении (1.94) микроскопический объем можно считать бесконечно малым, в то же время полагая, что точечная масса «размазана» по этому объему. Фактически мы производим сейчас переход от модели точечного распределения масс к модели сплошной среды, какой в действительности и является твердое тело благодаря большой его плотности. Произведенный переход позволяет в формуле (2.94) заменить суммирование по отдельным частицам интегрированием по всему объему тела:
![]() . (1.95)
. (1.95)
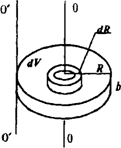
Рис. Вычисление момента инерции однородного диска
Здесь величины ρ и r являются функциями точки, например, ее декартовых координат.
Формула (1.95) позволяет вычислять моменты инерции тел любой формы. Вычислим в качестве примера момент инерции однородного диска относительно оси, перпендикулярной к плоскости диска и проходящей через его центр (рис.).
Поскольку диск однороден, плотность можно вынести из-под знака интеграла. Элемент объема диска dV = 2πr·b·dr, где b— толщина диска. Таким образом,
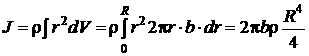 , (1.96)
, (1.96)
где R — радиус диска. Введя массу диска, равную произведению плотности на объем диска π·R2 b, получим:
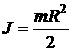 . (1.97)
. (1.97)
Нахождение момента инерции диска в рассмотренном примере облегчалось тем, что тело было однородным и симметричным, а момент инерции вычислялся относительно оси симметрии тела. В общем случае вращения тела произвольной формы вокруг произвольной оси, вычисление момента инерции может быть произведено с помощью теоремы Штейнера: момент инерции относительно произвольной оси равен сумме момента инерции J0 относительно оси, параллельной данной и проходящей через центр инерции тела, и произведения массы тела на квадрат расстояния между осями:
J=J0+ma2. (1.98)
Например, момент инерции диска относительно оси О' в соответствии с теоремой Штейнера:
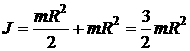 (1.99)
(1.99)
Поможем написать любую работу на аналогичную тему

