Энтропия - Шпаргалки по Физике

Мы убедились, что КПД необратимого кругового процесса всегда меньше, чем КПД при обратимом цикле. Этот результат можно сформулировать в следующем виде:

.

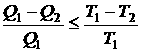Знак равенства соответствует случаю обратимых процессов. Отсюда нетрудно получить соотношение, которое играет важную роль в термодинамике:

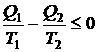.                                               (2.61)

Величина  называется энтропией. Она, как видно из полученного соотношения, остается неизменной при обратимом процессе и возрастает, если термодинамический процесс необратим. Энтропия — важная термодинамическая характеристика системы, такая же, как, например, внутренняя энергия. Утверждение, что при необратимых процессах энтропия замкнутой системы возрастает, составляет содержание второго начала термодинамики.

Возрастание энтропии системы при необратимом процессе выражает тот факт, что тепло само по себе не может переходить от менее нагретых к более нагретым телам. Последнее утверждение можно рассматривать также как формулировку второго начала термодинамики.

Из изложенного следует важный вывод. Поскольку КПД реальной тепловой машины всегда меньше, чем КПД идеальной машины (работающей по циклу Карно), а обязательным условием работы последней является необходимость отдавать тепло более холодному телу, становится очевидной невозможность создания так называемого вечного двигателя второго рода — устройства, осуществляющего круговорот тепла в природе и одновременно превращающего все полученное тепло в механическую работу.

Понятие энтропии имеет глубокий физический смысл, едва ли не больший, чем понятие энергии. Поскольку, как это следует из соотношения (2.61), энтропия остается постоянной при обратимом характере процесса и возрастает при необратимых процессах, энтропию рассматривают как меру необратимости термодинамического процесса. В состоянии термодинамического равновесия энтропия системы максимальна.

Рассмотрим, что представляет собой состояние термодинамического равновесия. В состоянии равновесия система однородна: все средние характеристики системы, такие, как концентрация, давление, температура, одинаковы во всех ее макроскопических частях. Равновесная система изотропна: в системе не существует направленного движения частиц или потока какой-либо другой физической величины. Иными словами, все направления движения равновероятны, и частицы совершают полностью хаотическое тепловое движение. Таким образом, состояние равновесия, с точки зрения статистической физики, представляет собой состояние полного беспорядка, в то время как состояние, отличное от равновесного, характеризуется существованием в системе направленного, т. е. упорядоченного движения. Указанное отличие равновесного состояния от неравновесного дает возможность рассматривать энтропию как количественную меру беспорядка, существующего в системе.

Беспорядочное либо упорядоченное расположение молекул в заданном объеме можно характеризовать количеством способов, которым можно расположить молекулы в этом объеме, не изменяя состояния системы. Ясно, что беспорядочно можно расположить молекулы значительно большим количеством способов

Состояния макроскопического тела (т.е. тела, образованного огромным количеством молекул) может быть задано с помощью объема, давления, температуры, внутренней энергии и других макроскопических (т. е. характеризующих все тело в целом) величин. Охарактеризованное таким способом состояние называется макросостоянием.

Состояние макроскопического тела, охарактеризованное настолько подробно, что оказываются заданными состояния всех образующих тело молекул, называется микросостоянием. Всякое макросостояние может быть осуществлено различными способами, каждому из которых соответствует некоторое микросостояние тела. Число различных микросостояний, соответствующих данному макросостоянию, называется статистическим весом или термодинамической вероятностью макросостояния. Таким образом, статистический вес представляет собой число микроскопических способов, которыми может быть осуществлено данное макросостояние.

Чтобы пояснить понятие статистического веса, рассмотрим способы, которыми молекулы газа могут распределяться между двумя половинами сосуда, в котором заключен газ. Пусть общее число молекул равно N. В качестве характеристики состояния газа примем число молекул, находящихся в левой половине сосуда, которое мы обозначим буквой n (соответственно число молекул в правой половине сосуда будет равно N — n). Состояние отдельной молекулы будем характеризовать указанием на то, в какой из половин сосуда она находится. Такое описание состояния газа и состояний отдельных молекул является, конечно, далеко не полным. Однако оно достаточно для того, чтобы выяснить на этом примере характерные особенности статистического поведения любых макросистем.

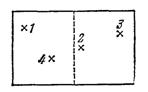Начнем со случая, когда полное число молекул равно четырем (рис.). Каждая молекула с равной вероятностью может находиться как в левой, так и в правой половине сосуда. Поэтому вероятность того, что, скажем, молекула 1 окажется в левой половине сосуда, равна 1/2. Пребывание в левой половине сосуда молекулы 1 и пребывание в той же половине сосуда молекулы 2 являются статистически независимыми событиями. Поэтому вероятность одновременного нахождения в левой части сосуда молекул 1 и 2 равна произведению вероятностей, т. е. (1/2)2. Продолжая эти рассуждения, получим, что вероятность одновременного нахождения в левой половине сосуда всех четырех молекул равна (1/2)4.

Аналогичные рассуждения дают, что вероятность любого размещения молекул в сосуде (скажем такого, при котором 1-я и 4-я молекулы будут находиться в левой половине сосуда, а 2-я и 3-я — в правой), также равна (1/2)4. Каждое из размещений представляет собой некоторое микросостояние газа. Из сказанного выше следует, что вероятность всех микросостояний одинакова и равна (1/2)4.

Таблица 1

В табл. 1 приведены все мыслимые способы распределения молекул между половинами сосуда (все микросостояния газа). Состояние, характеризуемое тем, что, скажем, в левой части сосуда находится одна молекула (безразлично какая), а в правой части — три молекулы, представляет собой макросостояние. Из таблицы видно, что такому макросостоянию соответствует 4 микросостояния. Следовательно, статистический вес данного макросостояния равен 4, а вероятность (обычная, а не термодинамическая) равна 4/16. Макросостояние, при котором в обеих частях сосуда находится одинаковое число молекул, реализуется с помощью шести микросостояний. Соответственно его статистический вес равен 6, а вероятность (обычная) равна 6/16.

Из рассмотренного примера вытекает, что все микросостояния данной системы равновероятны, вследствие чего статистический вес оказывается пропорциональным вероятности (обычной) макросостояния. Утверждение о равновероятности всех микросостояний лежит в основе статистической физики и носит название эргодической гипотезы.

Согласно табл. в случае четырех молекул имеется большая вероятность (равная 1/8) того, что все молекулы соберутся в одной из половин сосуда (левой или правой). Однако с увеличением числа молекул положение существенно меняется.

Найдем число способов (число микросостояний), посредством которых может быть осуществлено макросостояние, характеризуемое тем, что в левой половине сосуда окажется n молекул из общего числа их N, а в правой половине — (N — n) молекул. Для этого пронумеруем молекулы, приписав им номера от 1 до N. Затем станем отбирать по одной молекуле и помещать их в левую половину сосуда. Первую молекулу можно выбрать N способами, вторую — (N—1) способом, третью — (N—2) способами, наконец, n-ю молекулу можно выбрать (N— n+1) способом. Оставшиеся (N — n) молекул поместим в правую половину сосуда.

В результате для статистического веса получается выражение

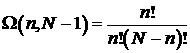
В табл. 2 приведены значения ω, вычисленные по формуле для случая N=24. Полное число способов распределения 24 молекул между двумя половинами сосуда равно 224=16 777 216, и только в двух случаях все молекулы оказываются сосредоточенными в одной из половин сосуда. Вероятность такого события равна примерно 10‑7. В четырех кубических сантиметрах воздуха содержится около 1020 молекул. Вероятность того, что все эти молекулы соберутся в одной из половин сосуда, равна двум, деленным на два в степени 1020, что составляет приблизительно . Эта вероятность настолько мала, что практически ее можно считать равной нулю.

Таблица 2

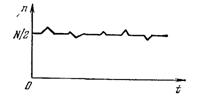На рис. изображен график, показывающий, как меняется число молекул n в одной из половин сосуда с течением времени. Это число колеблется около среднего значения, равного N/2.

Мы установили, что вероятность макросостояния (в дальнейшем мы будем говорить просто — состояния) пропорциональна его статистическому весу Q, т. е. числу микроскопических способов, которым может быть осуществлено данное макросостояние. Поэтому в качестве характеристики вероятности состояния можно было бы взять само это число, т. е. Q. Однако такая характеристика не обладала бы свойством аддитивности. Чтобы убедиться в этом, разобьем данную систему на две практически не взаимодействующие подсистемы. Пусть эти подсистемы находятся в состояниях со статистическими весами Q1 и Q2. Число способов, которым может осуществляться соответствующее состояние системы, равно произведению чисел способов, которыми могут быть осуществлены состояния каждой из подсистем в отдельности: Q = Q1∙Q2. Отсюда следует, что Q действительно не является аддитивной величиной.

Взяв логарифм от соотношения, получим lnQ = lnQ1 + lnQ2.

Откуда видно, что lnQ — аддитивная величина. Иметь дело с аддитивными величинами много проще и удобнее. Поэтому в качестве характеристики вероятности состояния принимается величина S, пропорциональная логарифму статистического веса. По причине, которая выяснится ниже, коэффициент пропорциональности выбирают равным постоянной Больцмана k. Определенную таким способом величину
                                               S = k∙lnQ                                                   (2.62)
называют энтропией системы.

Из сказанного в предыдущем параграфе вытекают следующие свойства энтропии:

1. Энтропия изолированной системы при протекании необратимого процесса возрастает. Действительно, изолированная (т. е. предоставленная самой себе) система переходит из менее вероятных в более вероятные состояния, что сопровождается ростом величины S.

2. Энтропия системы, находящейся в равновесном состоянии, максимальна.

Подчеркнем еще раз не абсолютно строгий характер высказанных утверждений. Например, энтропия системы, находящейся в равновесном состоянии, претерпевает незначительные кратковременные отрицательные флуктуации. Однако эти флуктуации столь малы, что практически энтропию можно считать постоянной и равной максимальному значению.

Утверждение о том, что энтропия изолированной системы может только возрастать (либо по достижении максимального значения оставаться неизменной), носит название закона возрастания энтропии или второго начала термодинамики. Иначе можно сказать, что энтропия изолированной системы не может убывать.

Итак, при протекании в изолированной системе необратимого процесса энтропия возрастает, т. е. выполняется соотношение dS > 0.

В общем случае dS³0.