Энтропия в обратимых и необратимых процессах.

Расчет энтропии для обратимых процессов. Продифференцируем выражение (15.4) и умножим его на T. Получим следующее равенство:

T·dSm = Cv·dT + R·T·dVm/Vm.     (15.6)

Для обратимых процессов справедливо уравнение Менделеева- Клапейрона. Следовательно, из уравнения (15.6) и выражения для расчета теплоемкости при постоянном объеме Cv = dU/dT, получим, что:

T·dSm = dUm + dAm = dQ.      (15.7)

В силу аддитивности величин S, V и U уравнение (15.7) справедливо для любой массы газа. Итак,

для любой массы идеального газа при протекании обратимых процессов изменение энтропии равно отношению количества теплоты, сообщенного системе к температуре системы.

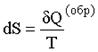.      (15.8)

Можно показать, что выражение (15.8) справедливо для любой термодинамической системы (не обязательно идеального газа). Для этого достаточно рассмотреть изолированную термодинамическую систему, находящуюся в равновесии и состоящую из идеального газа и произвольной подсистемы. Пусть температура идеального газа претерпит некоторую флуктуацию dT. Поскольку теплообмена с внешней средой не происходит, то количество теплоты отнятое от идеального газа - dQиг целиком сообщается подсистеме dQподсист. В силу малости dT этот процесс можно считать обратимым. При протекании в изолированной системе обратимого процесса ее энтропия остается постоянной и, следовательно, изменение энтропии будет равно нулю и dSподсист = - dSиг. Причем dSиг = dQиг/T. Поскольку температуры частей системы равны, а изменение энтропии идеального газа подчиняется выражению (15.8), то изменение энтропии подсистемы для обратимых процессов можно рассчитать с помощью выражения, аналогичного (15.8):

dSподсист = - dSиг = - dQиг/dT = dQподсист/T (обр.).

Итак, для обратимых процессов изменение энтропии термодинамической системы рассчитывается с помощью соотношения (15.9).

dS = dQ/T (обр.).     (15.9)

            Расчет энтропии для необратимых процессов. Состояние, реализуемое относительно малым числом способов называется упорядоченным. Состояние, реализуемое многими различными способами называется беспорядочным или случайным. Исходя из определения энтропии, можно сказать, что ее возрастание ведет к увеличению степени беспорядка системы.

Возрастать энтропия может по двум причинам:

- вследствие необратимого процесса перехода системы в равновесное (более вероятное) состояние;

- вследствие сообщения системе определенного количества теплоты.

Таким образом, для необратимых процессов справедливо следующее неравенство:

dS > dQ/T (необр.).     (15.10)

Смысл выражения (15.9) можно трактовать следующим образом. Сообщая определенное количество теплоты системе мы увеличиваем в ней долю беспорядка при данной температуре и, наоборот, увеличивая температуру, мы препятствуем возрастанию беспорядка макросистемы, обуславливаемого сообщаемым ей количеством теплоты.