Для выяснения понятий обратимый и необратимый процесс в термодинамическом смысле рассмотрим изотермическое расширение 1 моля идеального газа. Допустим, что 1 моль идеального газа находится в цилиндре, снабженном невесомым поршнем, который может передвигаться вдоль стенок без трения. Стенки цилиндра обладают идеальной теплопроводностью, т.е. во время процесса температура не меняется.
В начальный момент (рис. 3.1) газ занимает объем V1 и находится под давлением Р1. На графике такое состояние обозначено как начальное состояние 1.
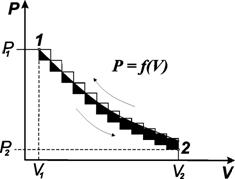
Рис. 3.1. Соотношение между Рвнеш и V, позволяющее определять работу расширения для газа, расширяющегося против постоянного внешнего давления Р2 и против переменного давления Р
Начнем изменять давление бесконечно малыми шагами. Если оно будет падать, то объем будет возрастать также бесконечно малыми шагами. Таким путем можно перейти из состояния 1 в состояние 2, в котором газ будет иметь давление Р2 и объем V2. Графически этот бесконечно медленный процесс изображается плавной кривой 2. Работа, совершаемая системой, ограничена изотермой с ординатами Р1 и Р2 и отрезком на оси абсцисс V2 – V1 . Это работа расширения газа. Обозначим ее W1-2. Представим себе обратный процесс, в котором мы будем путем бесконечно малого увеличения давления сжимать газ. В конечном счете мы сможем вернуть его в первоначальное состояние 1. Графически этот процесс будет описываться той же плавной кривой 2-1, но протекать в обратном направлении.
В этом случае система при переходе из конечного состояния в начальное будет проходить через те же промежуточные состояния давления и объема как в прямом, так и в обратном процессах. Изменения происходили на бесконечно малые величины, и система в каждый момент времени находилась в равновесном состоянии. В этом случае работа, которую совершает система в обратном процессе W2-1, будет равной, но обратной по знаку работе прямого процесса:
W12 = - W2-1; W12 + W2-1 = 0. (3.1)
Следовательно, обратимый процесс – это процесс, в результате которого система может возвратиться в исходное состояние без изменений в окружающей среде.
Значит, обратимые процессы протекают с бесконечно малыми скоростями. Только при этих условиях система в каждый момент времени будет находиться в состоянии, бесконечно мало отличающемся от равновесного. такие процессы называют равновесными, или квазистатическими.
Проведем процесс расширения 1 моль газа с конечной скоростью. при изменении давления на конечную величину (нижняя кривая) объем газа увеличивается также на конечную величину. Последовательно перейдем из состояния 1 в состояние 2. Графически этот процесс изображен ломаной линией. Работа расширения, которую при этом совершает газ, численно равна площади под ломаной линией. Она меньше, чем в предыдущем случае. Проведем процесс в обратном направлении. Здесь также давление будет увеличиваться на конечную величину (верхняя ломаная линия). Объем газа уменьшается и через некоторое время достигает равновесного состояния. Работа, которую при этом производит внешняя среда (работа сжатия), численно равна площади, ограниченной верхней ломаной линией, двумя ординатами Р1 и Р2 и отрезком на оси абсцисс V1 – V2 . Сопоставим диаграммы сжатия и расширения и отметим, что при изменении состояния газа с конечной скоростью работа обратного процесса по абсолютной величине больше работы прямого процесса:
|W1-2| <|-W2-1|, (3.2)
W1-2 + W2-1< 0. (3.3)
Возвращение системы из конечного состояния в начальное происходит по другому пути, и в окружающей среде остаются какие-то изменения.
Необратимый процесс – это процесс, после которого система не может возвратиться в исходное состояние без изменений в окружающей среде. При протекании необратимого процесса в каждый момент времени система не находится в состоянии равновесия. Такие процессы называются неравновесными.
Вывод: Все самопроизвольные процессы протекают с конечными скоростями и поэтому являются необратимыми (неравновесными) процессами.
Вывод: Работа, совершаемая системой в обратимом процессе, всегда больше, чем в необратимом:
Wобр > Wнеобр. (3.4)
Все реальные процессы в той или иной мере могут приближаться к обратимым. Работа, производимая системой, достигает максимального значения, если система совершает обратимый процесс:
Wобр = Wmax. (3.5)
Работу, производимую системой при переходе из одного состояния в другое, в общем случае можно представить как сумму работы расширения и других видов работы (работы против электрических, поверхностных, гравитационных и т.п. сил). Сумму всех видов работы, производимой системой за вычитом работы расширения, называют полезной работой. Если переход системы из состояния 1 в состояние 2 был осуществлен обратимо, то работа этого процесса будет максимальной (Wmax), а работа за вычетом работы расширения – максимальной полезной работой (W'max):
Wmax = W'max + pD V; (3.6)
W'max = Wmax - pD V. (3.7)
Поможем написать любую работу на аналогичную тему

