Ну и сразу такое определение: при достаточно хорошей симметрии напряжённость поля может быть найдена из уравнения ![]() . Значит, при достаточно хорошей симметрии поле всегда может быть найдено вот из этой интегральной теоремы. Ну, у нас это первое уравнение Максвелла. А теперь частные случаи.
. Значит, при достаточно хорошей симметрии поле всегда может быть найдено вот из этой интегральной теоремы. Ну, у нас это первое уравнение Максвелла. А теперь частные случаи.
1) Центральная (сферическая) симметрия. Пусть плотность заряда ![]() есть
есть ![]() . Значит, плотность, которая, вообще, функция координат точки
. Значит, плотность, которая, вообще, функция координат точки ![]() , зависит только от
, зависит только от ![]() , то есть только от расстояния до начала координат, это означает, что начало координат – центр симметрии. Вот эта формулка
, то есть только от расстояния до начала координат, это означает, что начало координат – центр симметрии. Вот эта формулка ![]() =
=![]() означает, что плотность на любой сфере радиуса r – константа, какая-то там плотность, ну, и отличная от нуля, на любой сфере она постоянна. Это означает, что распределение обладает сферической симметрией, и создаваемое им поле будет также обладать сферической симметрией. Отсюда следует, что
означает, что плотность на любой сфере радиуса r – константа, какая-то там плотность, ну, и отличная от нуля, на любой сфере она постоянна. Это означает, что распределение обладает сферической симметрией, и создаваемое им поле будет также обладать сферической симметрией. Отсюда следует, что ![]() (потенциал как функция точки) это есть
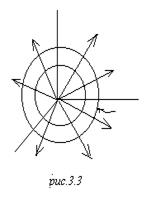
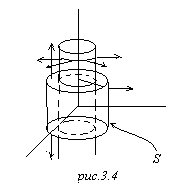
(потенциал как функция точки) это есть ![]() . Отсюда эквипотенциальные поверхности – сферы с центром в начале координат, то есть вот на любой сфере потенциал – константа. Отсюда далее следует, что силовые линии поля, которые являются всегда ортогональными к эквипотенциальным поверхностям, силовые линии поля – вот такие радиальные лучи:
. Отсюда эквипотенциальные поверхности – сферы с центром в начале координат, то есть вот на любой сфере потенциал – константа. Отсюда далее следует, что силовые линии поля, которые являются всегда ортогональными к эквипотенциальным поверхностям, силовые линии поля – вот такие радиальные лучи:
![]()
![]() Конструкция электрического поля может быть только такая. А теперь заметьте, здесь никакой специфики электричества не было, все эти выводы получены только из соображений симметрии. Любое векторное поле имело бы такую структуру, какая бы физическая природа у него ни была. Только сила соображения симметрии очень часто позволяет делать выводы безотносительно к конкретному предмету разговора.
Конструкция электрического поля может быть только такая. А теперь заметьте, здесь никакой специфики электричества не было, все эти выводы получены только из соображений симметрии. Любое векторное поле имело бы такую структуру, какая бы физическая природа у него ни была. Только сила соображения симметрии очень часто позволяет делать выводы безотносительно к конкретному предмету разговора.
![]() =
=![]() , отсюда дальше следует, что напряжённость поля на любой сфере
, отсюда дальше следует, что напряжённость поля на любой сфере ![]() может быть представлен так:
может быть представлен так: 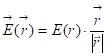 . Вот это
. Вот это ![]() , радиус-вектор, делённый на собственный модуль, есть единичный вектор
, радиус-вектор, делённый на собственный модуль, есть единичный вектор ![]() в направлении радиус-вектора. Всё. Пишем дальше эту формулу
в направлении радиус-вектора. Всё. Пишем дальше эту формулу ![]() . В качестве замкнутой поверхности, которая фигурирует в интеграле (поток вычисляется по замкнутой поверхности), выбираем сферу
. В качестве замкнутой поверхности, которая фигурирует в интеграле (поток вычисляется по замкнутой поверхности), выбираем сферу ![]() . Мы её (поверхность) можем брать любой, равенство от этого не зависит, но удобно взять
. Мы её (поверхность) можем брать любой, равенство от этого не зависит, но удобно взять ![]() . Пишем:
. Пишем: 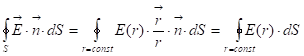 . Это равенство вследствие того, что
. Это равенство вследствие того, что ![]() ,
, ![]() - единичный вектор в направлении радиус-вектора (это вектор нормали к сфере, но нормаль к сфере в данной точке совпадает по направлению с радиус-вектором данной точки, эти векторы параллельны), а проекция радиус-вектора на самого себя – это его модуль, конечно,
- единичный вектор в направлении радиус-вектора (это вектор нормали к сфере, но нормаль к сфере в данной точке совпадает по направлению с радиус-вектором данной точки, эти векторы параллельны), а проекция радиус-вектора на самого себя – это его модуль, конечно, ![]() . Дальше,
. Дальше, ![]() во всех точках сферы одно и тоже, выносим за знак интеграла:
во всех точках сферы одно и тоже, выносим за знак интеграла: ![]() (вот это всё была математика, она к физике никакого отношения пока не имела, а физика – это следующее равенство), эта величина должна равняться интегралу от плотности заряда по объёму сферы, по которой вычисляется поток (интеграл от плотности по объёму это есть полный заряд внутри сферы):
(вот это всё была математика, она к физике никакого отношения пока не имела, а физика – это следующее равенство), эта величина должна равняться интегралу от плотности заряда по объёму сферы, по которой вычисляется поток (интеграл от плотности по объёму это есть полный заряд внутри сферы): ![]() , где
, где ![]() – заряд внутри сферы радиуса
– заряд внутри сферы радиуса ![]() . И это утверждение верно для сферы любого радиуса. Отсюда вывод – при центральной симметрии напряжённость поля во всех точках сферы радиуса
. И это утверждение верно для сферы любого радиуса. Отсюда вывод – при центральной симметрии напряжённость поля во всех точках сферы радиуса ![]() равна:
равна:
![]() ,
,
где ![]() - единичный вектор нормали к сфере. Эта формула, одна единственная, добивает все задачи центральной симметрии. Проблема одна – найти заряд, который находится внутри данной сферы, ну, это не очень тяжёлая проблема.
- единичный вектор нормали к сфере. Эта формула, одна единственная, добивает все задачи центральной симметрии. Проблема одна – найти заряд, который находится внутри данной сферы, ну, это не очень тяжёлая проблема.
Можем немножко продолжить это дело. Вследствие того, что на любой сфере ![]() , интеграл по объёму можно свести, в принципе, к однократному интегралу, интегрируя по шаровым слоям, ну, напишу тут без подробных комментариев
, интеграл по объёму можно свести, в принципе, к однократному интегралу, интегрируя по шаровым слоям, ну, напишу тут без подробных комментариев 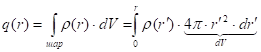 . Вот это
. Вот это ![]() объём шарового слоя радиуса
объём шарового слоя радиуса ![]() толщиной
толщиной ![]() . Почему я тут штрихи поставил, понятно.
. Почему я тут штрихи поставил, понятно. ![]() стоит в верхнем пределе интеграла, ну тогда, чтоб не путать переменную интегрирования с верхним пределом, там я вместо
стоит в верхнем пределе интеграла, ну тогда, чтоб не путать переменную интегрирования с верхним пределом, там я вместо ![]() пишу
пишу ![]() . Значит, если вот эта функция
. Значит, если вот эта функция ![]() предъявлена, то такой интеграл вычисляется. Так, всё, с центральной симметрией конец. Второй случай.
предъявлена, то такой интеграл вычисляется. Так, всё, с центральной симметрией конец. Второй случай.
![]()
![]()
![]()
![]()
![]() 2) Цилиндрическая симметрия. Вводим цилиндрические координаты
2) Цилиндрическая симметрия. Вводим цилиндрические координаты ![]() ,
, ![]() переходит в
переходит в ![]() . Вот у нас в цилиндрических координатах плотность
. Вот у нас в цилиндрических координатах плотность ![]() есть только функция от
есть только функция от ![]() , то есть не зависит от
, то есть не зависит от ![]() и не зависит от
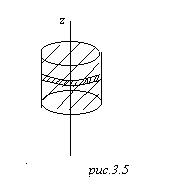
и не зависит от ![]() . Это означает, что имеется бесконечный цилиндр, и на поверхности цилиндра любого радиуса плотность заряда постоянна, и всё это дело продолжается до бесконечности по
. Это означает, что имеется бесконечный цилиндр, и на поверхности цилиндра любого радиуса плотность заряда постоянна, и всё это дело продолжается до бесконечности по ![]() , вот такая ситуация. Сразу, конечно ясно, что физически это не реализуется, но в качестве некоторой идеализации это разумно. Напишем снова
, вот такая ситуация. Сразу, конечно ясно, что физически это не реализуется, но в качестве некоторой идеализации это разумно. Напишем снова ![]() , значит, эквипотенциальные поверхности – это цилиндры с осью, совпадающей с осью симметрии, то есть с осью
, значит, эквипотенциальные поверхности – это цилиндры с осью, совпадающей с осью симметрии, то есть с осью ![]() . А силовые линии лежат в плоскостях ортогональных оси
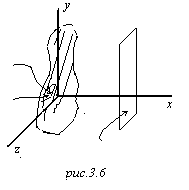
. А силовые линии лежат в плоскостях ортогональных оси ![]() . Так. В качестве замкнутой поверхности выбираем цилиндрическую поверхность радиуса
. Так. В качестве замкнутой поверхности выбираем цилиндрическую поверхность радиуса ![]() и высотой
и высотой ![]() , цилиндрическая поверхность, закрытая двумя крышками для того, чтобы она была замкнутой. Нормаль всегда берётся наружу. Из соображений симметрии ясно
, цилиндрическая поверхность, закрытая двумя крышками для того, чтобы она была замкнутой. Нормаль всегда берётся наружу. Из соображений симметрии ясно ![]() (напряжённость поля в любой точке цилиндрической поверхности направлена вдоль вектора
(напряжённость поля в любой точке цилиндрической поверхности направлена вдоль вектора ![]() , а величина зависит только от расстояния до оси симметрии). Поскольку у нас поверхность теперь задана в виде нескольких кусков, интеграл представится как сумма интегралов по этим кускам:
, а величина зависит только от расстояния до оси симметрии). Поскольку у нас поверхность теперь задана в виде нескольких кусков, интеграл представится как сумма интегралов по этим кускам: ![]() .
.
 Интеграл по крышкам равен нулю, потому что вектор
Интеграл по крышкам равен нулю, потому что вектор ![]() скользит по крышкам, скалярное произведение с нормалью – ноль.
скользит по крышкам, скалярное произведение с нормалью – ноль. ![]()
![]() .
.
![]()
![]() Внутренняя начинка этого цилиндра
Внутренняя начинка этого цилиндра ![]() , это интеграл по
, это интеграл по ![]() .
. ![]() , где
, где ![]() - это заряд на единицу длины цилиндра радиуса
- это заряд на единицу длины цилиндра радиуса ![]() , то есть это заряд лепёшки радиуса
, то есть это заряд лепёшки радиуса ![]() единичной толщины. Отсюда мы получаем результат:
единичной толщины. Отсюда мы получаем результат:
![]()
напряжённость поля во всех точках цилиндрической поверхности радиуса ![]() .
.
 Эта формула убивает все проблемы, связанные с цилиндрической симметрией. И, наконец, третий пункт.
Эта формула убивает все проблемы, связанные с цилиндрической симметрией. И, наконец, третий пункт.
![]()
![]() 3) Поле, создаваемое равномерно заряженной плоскостью. Вот мы имеем плоскость YZ, заряженную до бесконечности. Эта плоскость заряжена с постоянной плотностью s. s называется поверхностная плотность заряда. Если взять элемент поверхности
3) Поле, создаваемое равномерно заряженной плоскостью. Вот мы имеем плоскость YZ, заряженную до бесконечности. Эта плоскость заряжена с постоянной плотностью s. s называется поверхностная плотность заряда. Если взять элемент поверхности ![]() , то в нём будет заряд
, то в нём будет заряд ![]() . Значит, симметрия такова, что при сдвигах вдоль y и z ничего не меняется, это означает, что производные по y и z от чего угодно должны равняться нулю:
. Значит, симметрия такова, что при сдвигах вдоль y и z ничего не меняется, это означает, что производные по y и z от чего угодно должны равняться нулю: ![]() . Это означает, что потенциал есть функция x только:
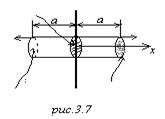
. Это означает, что потенциал есть функция x только: ![]() . Вот такое следствие. Это означает, что любая плоскость ортогональная оси x является эквипотенциальной поверхностью. На любой такой плоскости j=const. Силовые линии ортогональны этим плоскостям, значит силовые линии – прямые параллельные оси x. Из соображений симметрии следует, что, если здесь они идут вправо от плоскости, то слева они должны идти влево от плоскости (ожидается, что имеется зеркальная симметрия).
. Вот такое следствие. Это означает, что любая плоскость ортогональная оси x является эквипотенциальной поверхностью. На любой такой плоскости j=const. Силовые линии ортогональны этим плоскостям, значит силовые линии – прямые параллельные оси x. Из соображений симметрии следует, что, если здесь они идут вправо от плоскости, то слева они должны идти влево от плоскости (ожидается, что имеется зеркальная симметрия).
Вопрос, на самом деле, с зеркальной симметрией не такой простой. Вот ещё до не очень давнего времени, ещё на моей памяти, считалось, что зеркальная симметрия, конечно, имеет место в природе, что нет отличия между левым и правым. Но обнаружили в 60-х гг., что на самом деле такая симметрия не выполняется, природа отличает правое от левого. Будет ещё повод об этом поговорить. Но здесь это для нас выполняется.
![]()
![]()
![]()
![]()
![]()
 Пусть
Пусть ![]() – единичный вектор вдоль оси x. В качестве замкнутой поверхности берём цилиндр, прорезающий плоскость с двумя крышками. Напряжённости поля показаны на рисунке.
– единичный вектор вдоль оси x. В качестве замкнутой поверхности берём цилиндр, прорезающий плоскость с двумя крышками. Напряжённости поля показаны на рисунке.
![]() Интеграл по боковой поверхности ноль, потому что силовые линии скользят по боковой поверхности. Но как площади оснований цилиндра
Интеграл по боковой поверхности ноль, потому что силовые линии скользят по боковой поверхности. Но как площади оснований цилиндра ![]() . Если крышки взяты на одинаковых расстояниях от плоскости, то опять вследствие симметрии
. Если крышки взяты на одинаковых расстояниях от плоскости, то опять вследствие симметрии ![]() - функция расстояния до плоскости, тогда мы напишем так:
- функция расстояния до плоскости, тогда мы напишем так: ![]() . Тогда мы имеем:
. Тогда мы имеем: 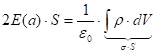 , а это заряд, который сидит внутри нашей поверхности.
, а это заряд, который сидит внутри нашей поверхности.
Отсюда получается: ![]() . Что мы видим, что длина цилиндра, ну, расстояние от крышек до плоскости, выпало из формулы, то есть на любом расстоянии от плоскости напряжённость поля одна и та же. Значит поле однородное. Напишем окончательно:
. Что мы видим, что длина цилиндра, ну, расстояние от крышек до плоскости, выпало из формулы, то есть на любом расстоянии от плоскости напряжённость поля одна и та же. Значит поле однородное. Напишем окончательно:
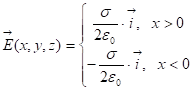
Эта формула автоматически учитывает и знак заряда: если. Вот эта формула даёт исчерпывающее описание поля заряженной плоскости. Если там не плоскость, а площадь конечной толщины, то поле надо разбить на тонкие пластины и вычислять.
Вот заметьте, для точечного заряда напряжённость поля убывает с расстоянием как ![]() , для цилиндра – как
, для цилиндра – как ![]() и для плоскости вообще не убывает.
и для плоскости вообще не убывает.
Два последние случая практически нереализуемые. Тогда какой смысл в этих формулах? Такой: например, эта формула справедлива вблизи середины плоского заряженного куска. Строго такая формула (однородное поле заполняет всё пространство) ни в какой физической ситуации не реализуется.
Поможем написать любую работу на аналогичную тему

