Щели Юнга

Проведем расчет интерференционной картины, полученной методом Юнга (пример пространственной когерентности).

В опыте Юнга источниками когерентных световых волн являются две щели S1  и  S2 в непрозрачном экране.

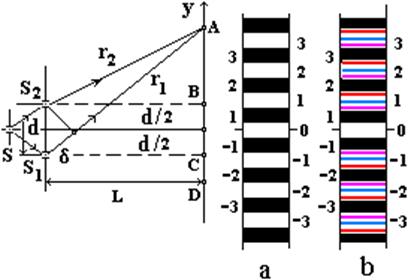 Эти щели, в свою очередь, освещаются щелью S от  протяженного источника   света  (рис. 2.4, а ; источник света не  показан).

                                                    Рис. 2.4.

Результат интерференции в некоторой точке А на экране (рис. 2.4) будет зависеть от оптической разности хода d = Dr = (r2- r1)n  и длины волны падающего света l.

Условия максимума и минимума интерференции, независимо от метода наблюдения,  известны. Запишем их в виде

                                               dмах = 2m,     dmin = (2m+1).

Наша задача состоит в том, чтобы, используя метод щелей Юнга, найти оптическую разность хода в интересующей нас точке на экране, например в точке А.

Если известны расстояние от щелей до экрана L, расстояние между щелями d, длина волны падающего монохроматического света l и абсолютный показатель среды n, то можно найти координаты максимума или минимума интерференционной картины в т. А.

Из треугольников S2АВ и S1АC, имеем

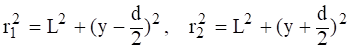                                                (2.26)

 или                                              .                                                   (2.27)

Из математики известно, что    , 

где разность r2 + r1 » 2L   (r » L, d<<L), а сумма r2 - r1= Dr =d, т.е.

                                         =2Ld.                                   (2.28)

Решив совместно (2.27) и (2.28), получим

                                         2уd » 2Ld    или   у@.                                        (2.29)    

При d=dмах = 2m из (2.29) получаем, что  координата максимума интерференции в точке наблюдения

                                                    умах =m l,                                                  (2.30)

где m = 0, ±1, ±2, ..., - порядок интерференции.

При d=dmin=(2m+1) из (2.29) находим, что  координата минимума интерференции  в точке наблюдения

                                                .                                          (2.31)

Таким образом,  на экране будет наблюдаться интерференционная картина в виде чередующихся светлых  (максимум) и темных (минимум) полос (рис. 2.4).

Согласно (2.8) и (2.29) распределение интенсивности, описываемое формулой

                                             J = 2J0(1+ cos)                                             (2.32)  

для у<<L,  d<<L, представляет собой серию максимумов одинаковой высоты. Это положение основано на том, что каждая щель одна равномерно освещает весь экран, что в действительности не выполняется.

Найдем ширину интерференционной полосы.

Например, максимум первого порядка (m=1) располагается между соседними минимумами первого и второго порядков, т.е.

                                             Dумах =у2min - у1min = ,                                          (2.33)

где на основании (2.31)      у1min=, (m=1);     у2min=,  (m=2).

Аналогично можно определить ширину интерференционного минимума, т.е. минимум любого порядка находится между соседними  максимумами.

Вывод: Ширина максимума и минимума интерференции в методе щелей Юнга одинакова.

Если щели Юнга освещаются белым светом, то на экране все максимумы образуют цветной спектр от красного до фиолетового, причем внутренний цвет - фиолетовый, а внешний - красный, кроме максимума нулевого порядка, где все цвета, складываясь, образуют белый цвет (рис.2.4, b).