Дифракция на щели

Различают два вида дифракции - дифракцию Френеля и дифракцию Фраунгофера в зависимости от соотношения между размерами тела, на котором происходит дифракция, и величиной зоны Френеля:    .

Дифракцию в параллельных лучах впервые наблюдал Фраунгофер.

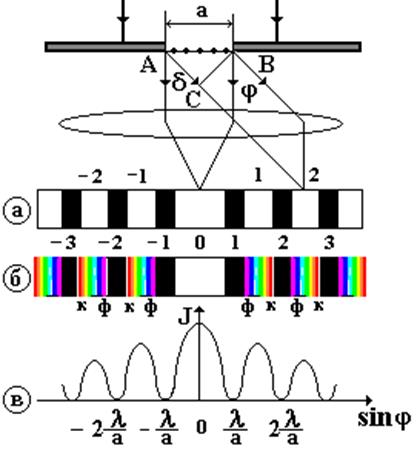
Пусть плоская монохроматическая волна падает на узкую щель в непрозрачном экране (рис. 3.4, а), где ширина щели много меньше ее длины (а<<);

                                           АС =  d = а sinj -

-         оптическая разность хода лучей от краев щели; ВС - фронт волны.

Рис. 3.4

                                                      Рис. 3.4.

При достижении фронтом волны щели,  в   соответствии  с   принципом Гюйгенса-Френеля, все точки щели становятся источниками вторичных волн, колеблющихся в одинаковой фазе. Все пространство за щелью будет охвачено волновым процессом, приводящим к дифракции света.

Найдем условия максимума и минимума дифракции света на щели для произвольного угла дифракции j. Для этого  разделим щель на зоны Френеля, которые будут иметь вид полос, параллельных ребру щели.

При интерференции света от  соседних зон щели результирующая амплитуда будет равна нулю, так как колебания в них происходят в противофазе.

Действительно, если      - есть число зон в щели, то при четном числе зон z = 2k, где k = 1, 2, 3, ...,  получаем условие минимума,

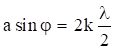                                                      .                                            (3.14)

При нечетном числе зон z=(2k+1) - условие максимума, т.е.

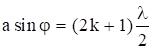                                                    .                                            (3.15)

Интенсивность света в точке, положение которой определяется углом дифракции j (рис. 3.4, в),  

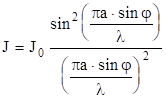                                 ,                                       (3.16)

где J0 - интенсивность света в центре дифракционной картины.

Угловое положение k-го максимума интенсивности дифракции на щели определяется по формуле

                                      .                                                    (3.17)

Следовательно, освещенность изменяется  вдоль экрана периодически с изменением j, обращаясь в нуль при значении угла j, для которых выполняется условие  минимума, т.е.    .

При некоторых значениях j освещенность достигает максимума, например, главный максимум наблюдается  при k=0  sinj=0, т.е. j=0.

При  данной ширине щели положение максимума и минимума зависит от l. Чем больше длина волны, тем больше расстояние между максимумами. Поэтому при  освещении щели  белым светом в центре дифракционной картины наблюдается белая полоса, так как главный максимум (нулевого порядка) является общим для всех длин волн. Максимумы же 1-, 2-, 3-го и т.д. порядков будут окрашены в цветные полосы от фиолетового до красного, симметрично расположенные относительно т. 0 (рис. 3.4,б).

Если световая волна падает на щель под углом a, то оптическая разность хода между крайними лучами d=а(sinj - sina). Поэтому условие дифракционного минимума записывается в виде 

                                  а(sinj - sina)=kl.                                (3.18)