Данные структурного корреляционного исследования представляют собой одну или несколько матриц “испытуемые” х “тесты”. Первичная обработка заключается в подсчете коэффициентов статистической связи между двумя и более переменными. Выбор меры связи определяется шкалой, с помощью которой произведены измерения.
1. Если измерения произведены по дихотомической шкале, то для подсчета тесноты связи признаков применяется коэффициент ср. Дихотомическая шкала – вырожденный вариант шкалы интервалов; для нее применимы все статистические методы шкалы интервалов.
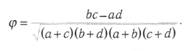
2. Данные представлены в порядковой шкале. Мерой связи, которая соответствует шкале порядка, является коэффициент Кэнделла. Он основан на подсчете несовпадений в порядке следования ранжировок X и У. Есть ряд испытуемых: сначала мы выстраиваем этот ряд в порядке убывания массы тела, а затем – в порядке убывания роста. Для каждой пары подсчитывается число совпадений и инверсий: совпадение, если их порядок по X и Y одинаков; инверсия, если порядок различен. Разница числа “совпадений” и числа “инверсий”, деленная на n (n– 1)/2, дает коэффициент используют коэффициент ранговой корреляции Спирмена, который является модификацией коэффициента Пирсона для натурального ряда чисел (рангов). Никакого отношения к порядковой шкале он не имеет. Но его рекомендуют применять в том случае, если одно измерение произведено по шкале порядков, а другое – по шкале интервалов.
Наконец, если исследователь полагает, что связи между переменными нелинейны, он вычисляет корреляционное отношение, характеризующее величину нелинейной статистической зависимости двух переменных.
Корреляционное исследование завершается выводом о статистической значимости установленных (или неустановленных) зависимостей между переменными. Однако перед психологами, – выяснить, не обусловлены ли связи между психологическими свойствами скрытыми факторами?
Поможем написать любую работу на аналогичную тему

