Взаимосвязь переменных

Обработка данных отдельно по каждой из переменных является, как правило, первым, исходным этапом анализа собранной информации. Вместе с тем наиболее интересные вопросы, занимающие социологов, связаны с одновременным анализом значений более одной переменной.

Обычный подход к анализу собранных данных предполагает формирование моделей типа: «социальные группы с разным уровнем образования (уровнем дохода, местом жительства и т.п.) отличаются по характеру проведения досуга (политическим предпочтениям, степени удовлетворенности жизнью и т.п.)». Другими словами, допускается, что существует переменная (скажем, принадлежность к определенной социальной группе), которая объясняет поведение других переменных. Таким образом, в этой модели у нас есть причина, и есть следствие. В традиционной терминологии объясняющие переменные называются независимыми, а объясняемые переменные—зависимыми.

В простейшем случае анализа двух переменных модель влияния представлена на рис. 3.1. Здесь влияние одной независимой переменной ставится в центр изучения, а влияние других переменных на зависимую переменную выступает в качестве причины, формирующей остатки, т.е. не объясняемую данной моделью часть поведения зависимой переменной. Если остаток невелик, можно считать, что наша модель описания поведения зависимой переменной с помощью независимой переменной достаточно точно объясняет собранные данные.

Функцию меры качества модели взаимосвязи переменных выполняют коэффициенты связи. Ниже мы подробно остановимся на коэффициентах связи, их особенностях и методах вычисления, но подход одинаков — чем выше коэффициент, тем больше взаимосвязь переменных, тем выше качество модели, и тем, соответственно, меньше остаток.

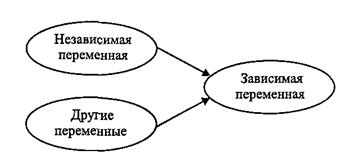
Рис. 3.1. Объясняющая модель поведения зависимой переменной

Двумерные таблицы

К наиболее часто используемым инструментам изучения взаимосвязи двух переменных относятся методы анализа таблицы сопряженности. Анализ таблицы является весьма простым и наглядным, и вместе с тем эффективным инструментом изучения одновременно двух переменных. Двумерная таблица сопряженности для переменных ql и q2 (табл. 3.1) составлена по данным исследования «Мониторинг социальных и экономических перемен в России», которые получены из ответов на вопросы:

q10  Как бы вы оценили в настоящее время материальное положение вашей семьи?

ql2 Как бы вы оценили в целом политическую обстановку в России?

Таблица 3.1.

Таблица сопряженности для переменных ql0 и ql2

В табл. 3.1 на пересечении строк и столбцов находятся числа, показывающие, какое количество единиц анализа (в данном случае — респондентов) обладают одновременно данными градациями по переменным q10 и ql2.  Внизу таблицы сопряженности располагаются суммарные данные по всем колонкам, а с правого края таблицы — аналогичные суммы по всем строкам. Иными словами, сбоку справа и снизу находятся одномерные частотные распределения для переменных, использованных в таблице.

Можно ли по данным табл. 3.1 сразу дать ответ на вопрос о наличии зависимости между переменными q10 и ql2? По всей вероятности, нет — стоящие в клетках таблицы числа ничего особенного не демонстрируют. Поставим вопрос иначе — а что, собственно, мы ищем? По всей видимости, при наличии зависимости между переменными q10 и ql2 при разных значениях переменной q10 поведение данных по переменной ql2 будет различным. Если говорить о примере табл. 3.1 — это значит, что респонденты, по-разному оценивающие свое материальное положение, будут по-разному оценивать политическую обстановку в России.

Если бы количество респондентов, имеющих различные значения переменной q10, было одинаковым, в табл. 3.1 можно было бы сравнивать между собой строки и оценить, насколько схожи значения в клетках, располагающихся в одной колонке. Однако количество респондентов по строкам сильно разнится, поэтому для такого сравнения построим таблицу, в клетках которой располагаются не абсолютные количества единиц анализа, а процент от сумм по строкам. Другими словами, число респондентов в каждой строке берется за 100% и от этого числа считается процент в каждой клетке таблицы. Таким образом, мы как бы нормируем каждую строку таблицы и получаем возможность сравнения распределений по строкам (табл. 3.2).

Таблица 3.2 показывает, что оценка политической ситуации в России значительно отличается по группам респондентов, по-разному оценивающих материальное положение своей семьи, и, следовательно, имеется определенная зависимость между переменными q10 и ql2.

При анализе зависимостей двух переменных важнейшим является вопрос о том, какую из переменных считать зависимой, т.е. подверженной влиянию, а какую — независимой, т.е. влияющей. В табл. 3.1 и в последующих рассуждениях предполагалось, что оценка материального положения семьи — независимая переменная, иными словами, она влияет на оценку политической ситуации, которая, следовательно, выступает зависимой переменной. Если мы поменяем местами переменные в модели и будем считать, что оценка политической ситуации оказывает влияние на оценку материального положения семьи, целесообразно изменить таблицу и проводить нормирование не in сумм по строкам, а от сумм по колонкам. Таблица 3.3 построена именно таким образом, т.е. использованы данные табл. 3.1, но нормированные по колонкам.

Таблица 3.2.

Таблица сопряженности переменных ql0 и ql2, %

Очевидно, что при решении вопроса о зависимости между переменными q10 и ql2 при анализе табл. 3.3 необходимо сравнивать распределения по разным колонкам таблицы, а не по строкам. Такое сравнение показывает, что среди респондентов, оценивающих политическую ситуацию и России как критическую, материальное положение своей семьи оценивают как плохое 49,1% респондентов (колонка 3, строка 3 табл. 3.3). В то же время среди оценивающих политическую ситуацию оптимистичнее, как напряженную, материальное положение своей семьи считают плохим 23,1% респондентов (колонка 3, строка 2 табл. 3.3).

Таблица 3.3.

Таблица сопряженности переменных ql0 и ql2, %

При анализе таблиц сопряженности крайне важно помнить, что мы, по сути дела, ищем наличие (или отсутствие) определенных статистических, а не причинно-следственных зависимостей. Вопрос о том, какая из переменных является причиной, т.е. оказывает влияние, а какая меняется вследствие этой причины, не может быть решен не только с помощью анализа таблиц, но и любым другим формально-статистическим методом. Это вопрос понимания той модели, которую мы проверяем методами построения таблиц либо другими статистическими приемами. Но результатом такой проверки не может быть утверждение: «наша модель верна», либо «наша модель неверна». Утверждать мы можем лишь то, что данные не противоречат (или, наоборот, противоречат) построенной модели, что само по себе отнюдь не является гарантией ее справедливости.

Иллюстрацию этой мысли можно найти у О. Генри. В рассказе «Вождь краснокожих» главный герой предложил изящную модель для ответа на вопрос о том, почему дует ветер — потому, что деревья шатаются. Если собрать данные о ветре и поведении деревьев во время ветра, любой статистический метод покажет, что данные ни в коем случае не противоречат этой модели, что, видимо, и послужило Джиму основанием для столь глубокомысленного вывода.

Построение таблиц сопряженности в пакете программ SPSS осуществляется с помощью команды Crosstabs.

Коэффициенты связи для номинальных переменных

В настоящее время существует множество числовых показателей для измерения степени и характера взаимосвязи двух переменных — коэффициентов связи. Наиболее известный из них — коэффициент .

Коэффициент

Оказывается, что сформулировать ответ на вопрос: что такое зависимость между ответами на два вопроса анкеты, удается довольно просто — от обратного. Другими словами, «зависимость есть отсутствие независимости». Этот, на первый взгляд, абсолютно не конструктивный ответ сильно продвигает нас вперед, поскольку в теории вероятностей существует строгий подход к определению независимости двух событий.

Два события считаются независимыми в том случае, если вероятность того, что они произойдут одновременно, равна произведению вероятностей того, что произойдет каждое из них.

Если в массиве данных социологического исследования оказалось - мужчин ½ и ⅓  лиц с высшим образованием, то при отсутствии зависимости между полом и образованием мужчин с высшим образованием в массиве должно быть ½ × ⅓ = 1/6. Поскольку массив данных уже собран, можно подсчитать, какая в действительности в нашем массиве доля мужчин с высшим образованием, и, если эта доля сильно отличается от 1/6, можно говорить, что гипотеза о независимости между полом и наличием высшего образования не подтверждается.

Таким образом, мы получаем некоторый инструмент количественной оценки степени независимости между двумя переменными. Если первый вопрос анкеты имеет три, а второй вопрос — два возможных варианта ответа, всего возможно шесть комбинаций ответов на эти им опроса. Для каждой из комбинаций мы можем вычислить вероятность ее (комбинации) появления в случае независимости этих переменных и реальную относительную частоту появления этой комбинации. Далее, находим разность между этими значениями для всех  этих шести возможных комбинаций.

Назовем то количество респондентов, которое должно быть в клетке таблицы в случае независимости двух событий, ожидаемой частотой. 1/2 *1/3*1000 = 166,7.

Как правило, реальные частоты  и  ожидаемые частоты разные во всех клетках. Следовательно, по нашему мнению, можно сделать вывод о том, что модель независимости переменных не подтверждается. Однако в простоте механизма получения такого важного вывода кроется определенная опасность. Ведь мы имеем дело со статистическими данными. Может быть, расхождения между реальными и ожидаемыми частотами носят случайный характер? Когда требуется делать те или иные выводы на основании статистических  данных, нам недостаточно простого сравнения нескольких чисел. Расхождения, равно как и совпадения этих чисел не могут служить достаточным основанием сколь-нибудь серьезных заключений.

Механизм проверки гипотезы о независимости переменных не сколько сложнее. Вычисляется показатель, фиксирующий степень расхождения реальных и ожидаемых частот, коэффициент  (хи-квадрат):

,

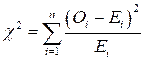где  — наблюдаемые частоты;  — ожидаемые частоты; n — число плеток в таблице.

Если бы мы получили  = 0, можно было бы однозначно говорить о точном совпадении этих частот, и, следовательно, о том, что модель независимости двух анализируемых переменных точно описывает реальные данные. Для случая же  > 0 хотелось бы найти какое-то точное значение Z, когда мы могли бы сказать: если  < Z,  маленький, можно считать, что отклонение наблюдаемых и ожидаемых частот незначительно и данные не противоречат модели независимости.

Сделать же это поможет то, что в математической статистик давно известно теоретическое распределение коэффициента  при условии, что в генеральной совокупности признаки независимы.  Теоретическое распределение коэффициента  рассчитаны для определенного числа степеней свободы , где N—число степеней свободы; r- число строк в таблице; с — число колонок.

Ограничения использования коэффициента . Важность метода проверки гипотезы о зависимости между переменными с использованием коэффициента  состоит в том, что в ходе построения этой модели не делают никаких опущений об уровне измерения самих переменных. Иными словами, можно использовать данный метод применительно к переменным, измеренным на любом уровне. Этот метод является чрезвычайно важным при обработке социологических данных, поскольку анкетная информация, в подавляющем большинстве случаев, содержит данные, измеренные на разных уровнях.

Однако одно ограничение применения коэффициента  все-таки есть. Доказано, что коэффициент  будет иметь теоретическое распределение  только в случае, когда ожидаемые частоты в таблице имеют значения 5 и более. Для корректного использования коэффициента  необходимо стремиться к тому, чтобы клеток с маленькими ожидаемыми частотами было как можно меньше.

Коэффициенты связи, основанные на

При использовании коэффициента  кроется неудобство, поскольку само по себе значение коэффициента ничего не значит. Действительно, информация о том, что  = 100, не говорит о наличии либо отсутствии взаимосвязи, поскольку для вывода об этом нужно еще знать число степеней свободы, а после этого необходимо заглянуть в таблицу критических значений распределения . Хотелось бы иметь такой коэффициент, глядя на значение которого, можно сразу, хотя бы приблизительно оценить наличие либо отсутствие связи.

Эту проблему увидел Пирсон, который предложил коэффициент С, производный от , само значение которого уже говорит о наличии либо отсутствии связи. Этот коэффициент носит название коэффициента сопряженности Пирсона:

,

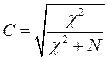где N—число опрошенных.

Как видно из формулы, с ростом значения  значение коэффициента С возрастает. При этом оно всегда больше нуля и меньше единицы. Недостатком коэффициента сопряженности Пирсона является то, что поскольку его значение зависит oт N, сравнивать между собой величины С для разных таблиц, как правило, нельзя.

Более распространен  коэффициент сопряженности Крамера, обозначаемый обычно как V.

,

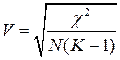где N— число опрошенных; К— наименьшее из чисел (r, с), где r — число строк; с — число столбцов.

Равно как и коэффициент сопряженности Пирсона С, коэффициент  V меняется от нуля до единицы. Оба коэффициента принимают значение нуль при нулевом значении , т.е. в ситуации, когда анализируемые переменные независимы. Однако, в отличие от коэффициента С, который всегда меньше единицы, коэффициент V равен единице в ситуации жестко детерминированной связи между переменными, т.е. в случае, когда одному значению переменной А всегда соответствует только одно значение переменной В.

Однако два этих граничных значения, с интерпретацией которых есть полная ясность, в практических исследованиях не встречаются. Что же означают те реальные значения коэффициента Крамера, с которыми обычно приходится иметь дело, скажем, 0,3? Ничего особенного это не означает, кроме того, что, по всей видимости, значение  достаточно велико и можно ожидать, что гипотеза о независимости анализируемых переменных не подтвердится. Интересно, что не существует таблиц критических значений для коэффициентов Пирсона или Крамера. Для того чтобы оценить уровень значимости этих коэффициентов, необходимо определить уровень значимости коэффициента , который, собственно, и лежит в их основе.

Как можно проинтерпретировать ситуацию, когда для одной пары переменных коэффициент Крамера равен, например, 0,2, а для другой — 0,5? Можно ли сказать, что вторая пара переменных сильнее взаимосвязана, чем первая?

Здесь мы фактически ввели понятие, которое используем в жизни ежедневно и которое, вроде бы, вполне очевидно — сила связи. Так вот, это интуитивное понимание силы связи никак не может быть применено для работы с коэффициентами связи в таблицах сопряженности. Большее значение , равно как и коэффициента Крамера, коэффициента Пирсона, либо какого-то иного, означает лишь уменьшение того уровня значимости , на котором отвергается гипотеза о независимости признаков. О характере же выявленной зависимости и о ее силе обсуждаемые коэффициенты ничего не говорят.

Коэффициенты связи, основанные на прогнозе

Поскольку «предсказание» в обыденной жизни ассоциируется, прежде всего, с предсказанием погоды, проиллюстрируем все вышесказанные примеры из этой области. Предположим, вероятность того, что в Москве будет идти снег в случайно выбранный день года, составляет 0,06. Однако зимой эта вероятность составляет уже примерно 0,2. Таким образом, зная значение переменной «время года» для случайно выбранного дня, мы можем гораздо точнее предсказывать вероятность того, что в этот день пойдет снег.

Логика коэффициента, фиксирующего улучшение предсказания значений одной переменной на основании значений другой переменной, весьма проста. Если назвать прогноз на основе значений только одной переменной первым прогнозом, а прогноз на основе двух переменных — вторым прогнозом, предлагаемые коэффициенты называются коэффициентами, основанными на модели прогноза:

Ошибка при первом прогнозе - Ошибка при втором прогнозе

Ошибка при первом прогнозе

Пока мы обсуждаем коэффициенты, основанные на прогнозе более часто встречающегося значения. Это так называемый прогноз модального значения. Коэффициенты для такого прогноза называются   (лямбда), их предложил Л. Гутман в 1941 г.

Что такое «первый прогноз» при модальном прогнозе? Это модальное значение предсказываемой переменной, обозначим его как А, а процент, который соответствует значению А, — как РrА. При таком обозначении ошибка при первом прогнозе будет Р1 = 1 -РrА.

При втором прогнозе мы анализируем по очереди каждую строку таблицы и выбираем в каждой строке модальную частоту. Пусть модальное значение в каждой строке будет Аi, а соответствующий процент — PrAi. Соответственно ошибка при предсказании значения в i-й строке составит Р=1-РrАi. Таким образом, ошибка при втором прогнозе будет средней ошибкой предсказания по каждой из строк таблицы:

/

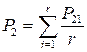Формула коэффициента, фиксирующего улучшение прогноза переменной, значение которой располагаются по столбцам таблицы, выглядит следующим образом:

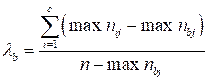
У обсуждаемого коэффициента есть одна особенность, отличающая его от коэффициента , В вычислении  строки и столбцы участвуют не симметрично. Разумеется, таблицу можно повернуть на 90% и с точки зрения содержащейся в таблице информации от этой операции ничего не изменится. При таком повороте не изменятся значения коэффициентов  и коэффициентов, основанных на . Однако значение коэффициента  изменится. Это связано с тем, что в модели коэффициента  мы предсказываем значение одной переменной на основании значений другой и переменные включены в модель не симметрично. Фактически одна переменная рассматривается как причина, а другая как следствие.

В этой связи наряду с переменной  которая фиксирует предсказание переменной, расположенной по колонкам таблицы, существует и переменная  , которая отражает улучшение предсказания переменной, расположенной по строкам на основании переменной, расположенной по столбцам. Наконец, когда мы не можем четко скачать, какая из переменных может рассматриваться как причина, а какая как следствие, существует так называемая  , т.е. «лямбда симметричная», представляющая полусумму  и .

Поскольку коэффициенты , так же как и  — статистические меры, то в их отношении встает задача оценки уровня значимости. При вычислении коэффициентов  в пакете SPSS в команде Crosstabs одновременно проводится вычисление уровней значимости а этих коэффициентов.

Достоинством коэффициентов  является то, что в отличие от коэффициента  либо производных от него само значение  и  имеет непосредственный смысл — это улучшение вероятности правильного предсказания. Иначе говоря, если для некоторой таблицы =0,2, это означает, что мы можем предсказывать модальное значение переменной, располагающейся по колонкам, зная совместное распределение двух переменных на 20% точнее по сравнению с ситуацией, когда мы не знаем этого распределения.

Однако это значение весьма условно. Действительно, коэффициенты  являются статистическими мерами и потому точное полученное значение коэффициента бессмысленно. Ведь мы можем повторить опрос для другой выборки (с соблюдением той же процедуры ее построения) и тем не менее почти наверняка получим другое значение коэффициента , поскольку будут опрашиваться другие респонденты. Следовательно, гораздо важнее получить не точечное значение коэффициентов , а доверительный интервал.

При вычислении коэффициентов  командой Crosstabs наряду с точечными значениями вычисляются также и величины стандартных ошибок. Стандартные ошибки позволяют построить доверительные интервалы с задаваемыми уровнями значимости.

Из приведенных формул коэффициентов  следует, что у них есть очень существенный недостаток — в том случае, когда все модальные частоты лежат в одной колонке либо в одной строке таблицы, соответствующие коэффициенты всегда обращаются в нуль. Таким образом, равенство нулю коэффициентов  и — это необходимое, но не достаточное условие для независимости переменных, образующих таблицу.

Последнее свойство весьма неудобно. Действительно, хотелось бы иметь коэффициенты, которые обладают естественным свойством — равенство нулю всегда говорит о независимости. Этим качеством обладают коэффициенты, также основанные на прогнозе, но в которых прогнозируется не модальная частота, а весь спектр частот. Это коэффициенты  (тау) Гудмена — Краскэла.

Коэффициенты связи  для порядковых данных

В предыдущих рассуждениях о таблицах сопряженности и коэффициентах связи не делалось никаких ограничений либо допущений в отношении уровня измерения тех переменных, которые образуют таблицу. Не использовалась и информация о порядке следования градаций в переменных. Очевидно, что если мы поменяем местами градации переменных, это никоим образом не скажется на значении коэффициентов , Крамера,  и .

Это является естественным для переменных, измеренных на номинальном уровне. Действительно, номера, которые присваиваются градациям в таких переменных, имеют абсолютно условный смысл. Так, совершенно не имеет значения, присвоен ли в вопросе «Ваш пол» мужчинам код 1, 2 или 28. Главное, чтобы код, присвоенный мужчинам, отличался от кода, присвоенного женщинам.

Однако эти рассуждения становятся неверными, когда речь заходит о переменных, измеренных на порядковом уровне. Для такого рода переменных порядок расположения градаций уже существен, поскольку он фиксирует степень выраженности измеряемого свойства. Измерение взаимосвязи в таблицах, построенных с использованием порядковых переменных, вполне возможно и нередко делается с использованием коэффициентов , Крамера,  и . Но эти коэффициенты не используют данные о порядке следования градаций и, следовательно, лишают нас возможности использовать всю содержащуюся в переменных информацию. Для того чтобы устранить этот недостаток, наряду с перечисленными коэффициентами, для порядковых переменных используют и другие меры связи — коэффициенты ранговой корреляции.

В настоящее время социологи используют коэффициенты ранговой корреляции —  Спирмена,  Кендэла,  Гудмена — Краскэла. Рассмотрим правила вычисления коэффициента  Гудмена — Краскэла как самого простого и часто используемого при анализе социологических данных.

На первом шаге вычисления коэффициента  фиксируют S—количества пар, в которых значение первой переменной не меньше значений второй переменной, и D — количества пар, в которых значение первой переменной не меньше значений второй переменной. Имея значения S и D, можно непосредственно рассчитать коэффициент  по формуле:

.

Из формулы  следует, что коэффициент  может изменяться в интервале от-1 до+1. Вообще, коэффициент у имеет прямую вероятностную интерпретацию — это разность между вероятностями правильного и неправильного порядка для пары случайно извлеченных из выборки наблюдений. Именно так следует понимать силу связи, которая фиксируется ранговыми коэффициентами корреляции. Поскольку для коэффициента у известно теоретическое распределение, то пакет SPSS одновременно со значением коэффициента вычисляет также и значение стандартной ошибки. Благодаря этому возможно построение доверительного интервала для коэффициента

Если необходимо решить задачу сравнения коэффициентов у, вычисленных для двух разных социальных совокупностей, необходимо:

•  определить доверительные интервалы для обоих коэффициентов;

•  посмотреть, пересекаются ли эти доверительные интервалы. Если они не пересекаются, то мы, с соответствующей доверительной вероятностью, можем утверждать, что эти коэффициенты различны.

Отличие ранговых коэффициентов корреляции от коэффициентов связи, основанных на  либо на модели предсказания, состоит в том, что фиксируют не только наличие либо отсутствие связи, но и, в случае наличия связи, ее направление. Это, несомненно, является достоинством данных коэффициентов, но в определенных случаях может являться и их недостатком. Дело в том, что ранговые коэффициенты корреляции фиксируют только однонаправленность, монотонность формы зависимости (см. рис.).

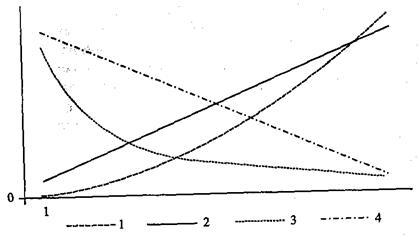
 Например, для всех изображенных на рис. 2.6 зависимостей имеем значение коэффициента у, равное +1 или -1, несмотря на то что сами формы зависимости существенно разные.

Что произойдет, если зависимость между переменными не имеет однонаправленной связи, как, например, зависимости, изображенные на рис.?

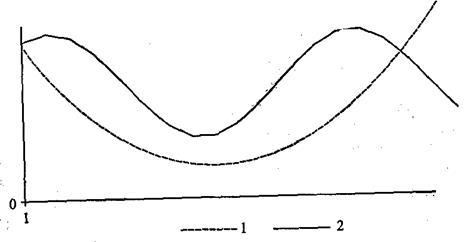
 Оказывается, что в ситуации такого рода форм зависимостей ранговые коэффициенты связи оказываются неэффективными. Действительно, если может оказаться, что для части респондентов, например тех, кто имеет малые значения переменной х (рис. график 1), значение рангового коэффициента связи будет отрицательное, а для тех респондентов, которые имеют большие значения переменной х, значение рангового коэффициента будет положительное, то общее значение рангового коэффициента может оказаться равным нулю. И это при том, что, как показывает график, связь между переменными явно есть.

Таким образом, тот факт, что значение рангового коэффициенту корреляции равно нулю, говорит не об отсутствии связи, а лишь об отсутствии монотонной связи.

Если при изучении взаимосвязи двух порядковых переменных мы получили нулевое значение коэффициента ранговой корреляции, встает вопрос о том, как можно проверить, с какой из ситуаций мы имеем дело: между переменными вообще нет зависимости, или нет монотонной зависимости? Ответ достаточно прост: следует посчитать, скажем, коэффициент . Если этот коэффициент покажет наличие связи при нулевом значении коэффициента у, очевидно, что мы имеем дело с наличием немонотонной связи между переменными.

Коэффициент корреляции Пирсона

В том случае, когда обе анализируемые переменные измерены по метрическим шкалам (интервальным либо абсолютным) появляется дополнительная возможность измерения степени взаимосвязи между этими переменными — это коэффициент корреляции Пирсона. Формула для вычисления этого коэффициента корреляции достаточно проста:

,

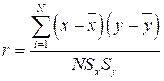где х и у — средние значения переменных х и у соответственно; Sx и Sy — стандартные отклонения переменных х и у; N — количество наблюдений.

Из формулы следует, что коэффициент г фиксирует степень того, насколько переменные х и у одновременно отклоняются от средних значений. Таким образом, в отличие от ранговых коэффициентов корреляции, которые замеряют монотонный характер связи между переменными, коэффициент корреляции Пирсона учитывает более узкий характер монотонности — линейность. Когда между переменными есть строгая линейная зависимость, значение коэффициента корреляции Пирсона будет равно +1 в случае положительной связи и -1 в случае отрицательной связи.

Когда мы рассматриваем совместное поведение двух метрических переменных, то целью социологического анализа является установление взаимосвязи, зависимости между этими переменными. При использовании для решения этой задачи коэффициента корреляции Пирсона следует помнить, что нулевое значение этого коэффициента, строго говоря, свидетельствует только об отсутствии линейной зависимости. Это, в свою очередь, может свидетельствовать и об отсутствии вообще какой-либо зависимости, и о том, что зависимость есть, но она носит нелинейный характер. Установить с помощью данного коэффициента, с какой из этих ситуаций мы имеем дело в конкретном случае, нельзя. После вычисления коэффициента Пирсона для данных социологического опроса, как и в случае ранговых коэффициентов корреляции, возникают две взаимосвязанные статистические задачи:

• является ли полученная величина коэффициента статистически значимой;

• каков доверительный интервал для полученного значения.

Команда Crosstabs, в случае запроса на вычисление коэффициента корреляции Пирсона, выводит таблицу, которая позволяет решить обе задачи.