Описательная статистика

Прежде всего рассмотрим простейшие количественные методы анализа данных. В зависимости от решаемых задач разделим их на три основных типа.

1. Одномерный описательный анализ раскрывает некоторые характеристики частотных распределений.

2. Двумерный описательный анализ связан с описанием формы и силы взаимосвязи между переменными, а также со сравнением значений некоторой переменной в разных социальных группах.

3.  Объяснительный анализ направлен на выявление силы влияния переменных друг на друга.

Построение частотных распределений

Анализ частотных распределений результатов количественного социологического исследования — это первый шаг при обработке собранной информации. Во многих случаях этот анализ не является, строго говоря, анализом данных, а выполняет функции получения общих представлений об изучаемых социальных группах.

Первый шаг одномерного описательного анализа для объяснения какого-то явления — его описание. Результаты любого массового опроса содержат ответы большого числа респондентов на широкий круг анкетных вопросов. Даже в рамках только одного вопроса анкеты объем исходной информации достаточно велик для того, чтобы можно было охватить его одним взглядом и каким-то образом суммировать. Именно задачу сжатия исходной информации, компактного ее представления для дальнейшего осмысления и решают методы одномерного описательного анализа.

Одномерный описательный анализ решает поставленную задачу взаимодополняющими методами:

• построения частотных распределений;

• графического представления поведения анализируемой переменной;

• получения статистических характеристик распределения анализируемой переменной.

Использование статистических характеристик для анализа одномерных распределений

Одной из важнейших характеристик при описании поведения отдела ных переменных является показатель средней тенденции. В курсе «Методы социологического исследования» подробно обсуждаются вопросы уровней измерения, используемые в социологических анкетах, а также рассматриваются возможности применения различных мер центральной тенденции для показателей с разным уровнем измерения.

Возможности использования различных мер средней тенденции цля шкал различного типа приведены в табл. 2.1.

Таблица 2.1.

Возможности использования различных мер средней тенденции для шкал различного типа

Рассмотрим специфику использования мер средней тенденции для анализа социологических данных на примере среднего арифметического. Среднее арифметическое широко используется в повседневной жизни и не нуждается в дополнительных рекомендациях. Вместе с тем использование только среднего арифметического для описания значений переменной таит определенную опасность.

Говоря о среднем значении некоторой переменной мы, по сути дела, заменяем рассмотрение всей совокупности значений этой переменной единственным показателем, фактически предполагая, что значение этого показателя достаточно хорошо описывает поведение анализируемой переменной. Очевидно, что в данном случае среднее значение выступает в качестве определенной модели значений переменной.

Несомненно, что среднее арифметическое переменной представляет совокупность значений этой переменной неполно и с возможными ошибками. Зная, например, среднее значение зарплаты среди совокупности опрошенных, мы не можем достаточно точно определить зарплату того или иного респондента. Только в том случае, когда все значения переменной одинаковы, среднее значение абсолютно точно отражает поведение переменной. Во всех других случаях среднее арифметическое как модель переменной является моделью неточной. Следовательно, для нас важно знать не только значение данной модели, но и степень точности, качества этой модели.               

Рассмотрим данные о заработной плате пяти респондентов, лученные в ходе социологического исследования (табл. 2.2).

Таблица 2.2.

Данные о средней заработной плате, средне значение заработной платы, расхождение среднего и фактических данных

Данные, приведенные в табл. 1.5, можно представить в виде условной формулы:

Реальные данные = Модель + Остаток.

Расхождение реальных данных и модели в этой формуле называется остатком.

В каком случае модель средней зарплаты будет с небольшой погрешностью описывать реальные данные? Ключевым вопросом при анализе данных с помощью какой бы то ни было модели является оценка того, насколько хороша модель. Остатки дают нам эффективный инструмент для оценки качества модели: очевидно, что модель тем лучше, чем меньше остатки.

Таким образом, наряду со средней характеристикой, которая удобна тем, что дает нам картину (вернее, часть картины) поведения значений переменной, целесообразно иметь и еще одно число, которое оценивало бы качество средней как модели. Функции такой характеристики выполняют меры разброса, наиболее известна среди них дисперсия. Фактически дисперсия представляет собой не что иное, как сумму квадратов остатков, деленную на количество наблюдений:

,

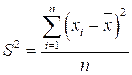где  — значение переменной х для i-го респондента;  — среднее значение переменной х; n — количество опрошенных респондентов. Недостатком дисперсии является то, что эту величину трудно и ценить интуитивно. Данные, представленные в табл. 2.2, имеют понятные нам единицы измерения — рубли. Поэтому мы сразу можем оценить, что за величина остатка, скажем, у респондента 4 — 500 руб. Понятна нам и размерность среднего показателя — 15 500 руб. Мы можем интерпретировать это значение, соотнося его с нашим знанием социальной действительности.

В то же время значение дисперсии для данных табл. 2.2 составляет 4 000 000. Едва ли мы можем, хотя бы на качественном уровне, оценить, большая эта величина или маленькая. Это значение не дает нам ответа на главный вопрос — хороша ли наша модель среднего арифметического, т.е. средней зарплаты. Причина того, что дисперсия плохо приспособлена для ответа на вопрос о качестве модели среднего, в том, что остатки берутся в квадрате. Для того чтобы преодолеть это затруднение, используют два производных от дисперсии показателя — стандартное отклонение и стандартная ошибка среднего.

Стандартное отклонение — это корень квадратный из дисперсии. Стандартное отклонение для данных табл. 2.2 — 2000.

.

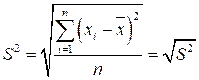Стандартная ошибка среднего (с.о.) тоже широко используется для решения задачи оценки качества среднего как модели с несколько иной стороны: она дает возможность соотнести величину  с генеральным математическим ожиданием. Последнее с вероятностью 0,95 лежит в интервале ( ± 2с.о.).

.

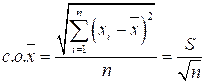По табл. 2.2 значение стандартной ошибки среднего составлявяет 894. Таким образом, можно утверждать, что с вероятностью 0,95 математическое ожидание зарплаты должно лежать в интервале 15 500 ± 2894, или от 13 712 до 17 288 руб.

Подводя итог, необходимо подчеркнуть, что использование среднего арифметического без указания одного из показателей качества среднего как модели (дисперсии, стандартного отклонения, либо стандартной ошибки среднего) не дает возможности удовлетворительной интерпретации полученного среднего.

Проведенные рассуждения о необходимости дополнения характеристики средней тенденции показателем качества этой модели справедливо и в отношении тех переменных, которые измерены на номинальном или порядковом уровне. Для номинальных переменных мерой центральной тенденции может выступать только мода, т.е. наиболее часто встречающееся значение переменной. Мода не имеет какого-то показателя разброса. Определенной характеристикой может считаться лишь само процентное значение модальной величины. В качестве примера рассмотрим табл. 2.3, в которой приведено одномерное частотное распределение респондентов, проживающих в населенных пунктах разного типа.

В табл. 2.3 модальным значением является «2». Тот факт, что на, эту градацию приходится 53,7% всех опрошенных респондентов, говорит о том, что на все остальные градации приходится лишь 46,3%, что может указывать на разброс значений. Однако данное указание достаточно слабо, поскольку не показывает, как именно разбросаны данные по другим градациям анализируемой переменной.

Для переменных, измеренных на порядковом уровне, основной мерой центральной тенденции является медиана. Рассчитаем медиану для переменной q23: Насколько вы удовлетворены состоянием своего здоровья?, которая фиксирует ответы респондентов по 7-балльной порядковой шкале (табл. 2.4).

Таблица 2.3.

Одномерное частотное распределение переменной

CITY «Тип населенного пункта»

Медиана является такой точкой на шкале, которая делит всю совокупность опрошенных на две равных части — тех, кто отметил градации меньше этой точки (либо равные ей), и тех, кто отметил градации больше этой точки. Из табл. 2.4 видно, что в вопросе q23 градации 1, 2, 3 и 4 отметили 50,4% респондентов, и, следовательно, радация «4» является медианой.

Таблица 2.4.

Одномерное частотное распределение переменной q23

Наиболее распространенным показателем, характеризующим разброс значений переменной, измеренной на порядковом уровне, является квартильное отклонение. Чтобы понять смысл этого показателя, необходимо уяснить значение понятия квартиля.

Квартиль является естественным развитием медианы, с той разницей, что квартильное разбиение делит всех респондентов не на 2, а на 4 части. Первый квартиль — это такая точка на шкале, значения меньше (либо равные) которой отметили 25% опрошенных. Второй квартиль — точка, меньше которой отметили 50% опрошенных (следовательно, второй квартиль совпадает с медианой). Наконец, третий квартиль — точка, градации меньше которой отметили 75% опрошенных.

В примере табл. 1.7 первый квартиль — это градация «2» переменной q29, поскольку градации «1» или «2» отметили 25,1% опрошенных. Второй квартиль (медиана) — «4», а третий квартиль — градация «6». Квартильное отклонение — это разница между третьим и первым квартилями. В рассматриваемом примере квартильное отклонение равно 4. При том что в целом рассматриваемая переменная q23 имеет 7 градаций, квартильное отклонение, равное 4, может рассматриваться как достаточно большое, если рассматривать шкалу как метрическую, можно сделать вывод, что модель средней тенденции (в данном случае — медиана) неточно отражает поведение переменной, поскольку много респондентов имеют значения переменной, существенно отличающиеся от медианы.

Обдумывая логику разбиения совокупности значений переменной на 2 (медиана), либо на 4 (квартили) равнонаполненных части, вполне можно поставить задачу разбиения и на 5, и на 10, и вообще на любое количество равных частей. Действительно, при анализе социологических данных иногда используются квинтильное (на 5 равных частей) и децильное (на 10 равных частей) разбиения. Соответственно применительно к таким разбиениям можно использовать такие меры разброса, как квинтильное и децильное отклонения.

Полезным и нередко используемым показателем при анализе количественных переменных является децильное отношение. Продемонстрируем использование данного показателя на примере. В ходе социологического исследования респондентам, в частности, задавался вопрос о размере их заработной платы на основном месте работы. При анализе данного показателя возникла потребность изучить, насколько высока неоднородность значений получаемой респондентами заработной платы.

В качестве первого шага для решения этой задачи было построено децильное разбиение исследуемого показателя (табл. 2.5).

Таблица 2.5

Децильное разбиение для переменной «Размер вашего заработка за последний месяц»

Материалы табл. 2.5 говорят о том, что заработную плату до 1800 руб. получают 10% опрошенных (граница первого деци-ля), а также о том, что 10% опрошенных получают зарплату в размере 15 000 руб. и выше (граница десятого дециля).

Децильное отношение — это отношение десятого дециля к первому. Этот показатель демонстрирует, во сколько раз больше получают 10% наиболее высокооплачиваемых респондентов по сравнению с 10% наименее оплачиваемых. В нашем примере децильное отношение составляет 8,3, что показывает степень неоднородности заработной платы.

Стандартизация показателей

Одной из задач, возникающих при одномерном анализе социологических данных, является сопоставление значения определенной переменной для конкретного респондента со средним значением этой переменной в какой-то социальной группе. Например, если результаты опроса показали, что некий респондент за последний месяц потратил /0 руб. на покупку хлеба, и не зная средней величины затрат на покупку данного вида товаров в том регионе, где проживает респондент, мы не можем сказать, много или мало денег потратил респондент на хлеб. Величина «70 рублей» может быть осознана и проинтерпретирована только в сравнении с затратами других респондентов. Для того чтобы сразу оценить относительную величину того или иного количественного показателя для конкретного респондента, ис пользуется метод стандартизации исходных данных.

Существует несколько различных подходов к стандартизации данных, но самый распространенный — это так называемая Z-стандартизация. Вычисление стандартизованной величины Zxi для значения переменной х для i-го респондента проводится по формуле

,

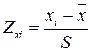где — значение переменной для i-го респондента; — среднее значение переменной х; S— стандартное отклонение для переменной х.

Значение показателя  для i-ro респондента более информативно с точки зрения задачи относительного положения данного респондента, чем значение исходной переменной . Действительно, из формулы следует, что если для i-го респондента  положительно, данный респондент имеет значение переменной х. большее, чем средний опрошенный респондент. Таким образом, знак Zxi сразу говорит нам о положени респондента (по переменной х) относительно других опрошенных.

После того как мы выяснили, большее или меньшее значение и переменной х имеет данный респондент по сравнению с другими опрошенными, необходимо узнать, насколько это значение больше или меньше, чем у других респондентов. Из свойств стандартного нормальной распределения следует, что 68% Zxi должны лежать в интервале от -1 до 1, а 95% — в интервале от -2 до 2. Таким образом, если по модулю значение Z. меньше единицы, мы можем сказать, что значение переменной х для данного респондента вполне типично. Если значение  по модулю находится от 1 до 2, можно говорить, что данный респондент по рассматриваемому показателю значительно отличается от среднего респондента. Наконец, если  по модулю превосходит 2, можно утверждать, что данный респондент резко отличается от среднего.

Использование стандартизованных переменных весьма полезно и при решении задачи сопоставления показателей, измеренных в разных единицах. Например, в нашем распоряжении есть данные по опросам в России и США, и получается, что у российского респондента А средняя зарплата составляет 9000 руб. в мес, а у американского респондента В — 2000 долл. в мес. Очевидно, что, не зная значений средней зарплаты в России и США, мы не можем сказать, выше ли респондент А респондента В, с точки зрения средней заработной платы, в их социальном кругу.

Если у нас есть возможность сопоставлять не исходные данные о величинах зарплат, а соответствующие стандартизованные показатели, мы легко можем ответить на поставленный вопрос.

Интервальное оценивание

Одномерное частотное распределение позволяет констатировать определенные закономерности в той совокупности респондентов, которые были опрошены в ходе проведенного исследования. Однако объектом социологического исследования выступает, в абсолютном большинстве случаев, не та совокупность респондентов, которая непосредственно опрашивается, а какая-то социальная либо социально-демографическая группа. Опрошенные респонденты выступают лишь кик представители этой группы, как выборка, которая призвана репрезентировать поведение группы в целом. Поэтому возникает закономерный вопрос: как соотносится одномерное распределение, характеризующее поведение той или иной переменной в выборочной совокупности, с поведением этой переменной во всей анализируемой социальной общности? Иными словами, как можно перенести результат, полученный для выборки, на всю изучаемую генеральную совокупность?

Поскольку размер обследованной выборочной совокупности существенно меньше, чем генеральная совокупность, то перенесение результатов с выборочной совокупности на генеральную возможно шиш. с определенной точностью. Иными словами, если в ходе опроса получено, что в выборочной совокупности 6,9% опрошенных отвечали, что они «в целом довольны своей жизнью», это вовсе не значит, что во всей генеральной совокупности своей жизнью довольны именно 6,9% населения. Выборочный метод дает нам правило, которое позволяет, зная значение определенного параметра в выборочной  совокупности, оценить возможное значение этого параметра в генеральной совокупности.

Теоремы математической статистики говорят нам, что если выборка исследования реализуется с соблюдением определенных требований, результаты, полученные на выборке, могут быть перенесены на генеральную совокупность доверительных интервалов. Таким образом, если в выборочной совокупности оказалось 6,9% респондентов, довольных своей жизнью, в генеральной совокупности таких респондентов будет (6,9 ± Δ)%. Величина Δ называется максимальной ошибкой выборки, а интервал (6,9 - Δ, 6,9 + Δ) — доверительным интервалом; Δ вычисляется по формуле

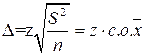
где z — критические точки нормального распределения; S2 — дисперсия анализируемого показателя; n — объем выборки.