Для простоты рассмотрим одномерные нерелятивистские квантовые системы, состоящие из одной частицы. Состояние системы полностью описывается волновой функцией 
. Поскольку частица может находиться в любой точке пространства, то 
–
вероятность того, что частица находится в элементе «объема» dx
с центром в точке х в момент времени t, – равна:
где С – нормировочная постоянная. Вероятностная интерпретация 
означает, что удобно использовать нормированные волновые функции, удовлетворяющие условию:
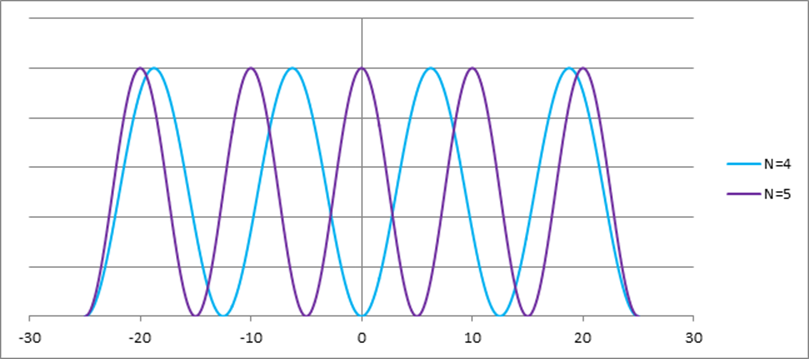
Тогда постоянная С в выражении (3.1) равна 1.
Если частица движется в потенциале U
,
то временная эволюция функции 
описывается нестационарным уравнением Шредингера
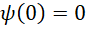
Физические величины, такие, как импульс, можно представить операторами. Математическое ожидание, или среднее значение наблюдаемой величины А определяется выражением:
где 
оператор, соответствующий величине А.
Например, оператор, соответствующий импульсу P, имеет вид 
.
Если потенциал не зависит от времени, то для уравнения (3.3) можно получить решения вида:
Частица, находящаяся в состоянии (3.5), имеет вполне конкретное значение энергии Е. Если подставить выражение (3.5) в (3.3), то получим стационарное уравнение Шредингера
Заметим, что 
– собственная функция оператора Гамильтона (гамильтониана)
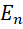
соответствующая собственному значению Е, т.е.
Общее решение можно выразить в виде суперпозиции собственных функций оператора, отвечающего той или иной физической наблюдаемой величине. Например, если Н не зависит от времени, то можно записать
где 
– собственные функции оператора Н, а знак ∑ обозначает сумму по всем дискретным состояниям и интеграл по непрерывному спектру. Коэффициенты 
в формуле (3.9) можно определить из значения в любой момент времени t.
Например, если нам известна при 
, то можно воспользоваться свойством ортогональности собственных функций любого физического оператора и получить:
Коэффициент можно интерпретировать как амплитуду вероятности измерения полной энергии, при котором получается значение 
.
Рассмотрим решения стационарного уравнения Шредингера (3.6), соответствующие связанным состояниям. Основной результат будет заключаться в том, что допустимые решения уравнения (3.6) существуют только тогда, когда собственные значения квантованы, т.е. ограничены дискретным набором энергий. Чтобы решение было допустимым, функции 
должны быть конечны для всех значений x
и ограничены для больших значений |x| так, чтобы функцию можно было нормировать. Для конечной функции 
требуется, чтобы функции и 
были непрерывны, конечны и однозначны для всех
х.
Поскольку стационарное уравнение Шредингера является дифференциальным уравнением второго порядка, то для получения единственного решения необходимозадать два краевых условия. Для упрощения анализа рассмотрим симметричные потенциалы, удовлетворяющие условию
Как следует из условия (3.11), можно считать, что функции
обладают определенной четностью. Для четных решений 
; нечетных решений 
.
Определенная четность позволяет задать либо 
либо 
при х = 0.
Чтобы был понятен выбор подходящего алгоритма численного решения уравнения (3.6), напомним, что решение (3.6) с U
можно представить в виде линейной комбинации косинусов и синусов. Колебательный характер этого решения позволяет надеяться, что алгоритм Эйлера – Кромера, рассмотренный ниже, будет давать удовлетворительные результаты и в случае U
. Алгоритм Эйлера – Кромера реализуется следующим образом:
1. Разбиваем область изменения х на N отрезков длиной ∆x.
Введем следующие обозначения: 
и 
2. Задаем четность функции .
Для четного решения выбираем 
и 
; для нечетного выбираем 
и 
. Ненулевые значения 
и произвольны.
3. Задаем начальное приближение для Е.
4. Вычисляем 
и 
используя алгоритм:
5. Проводим итерации по возрастанию х до тех пор, пока не начнет расходиться.
6. Изменяем величину Е и повторяем шаги (2) – (4). Окаймляем значение Е, изменяя его до тех пор, пока при значении Е чуть меньше текущего не будет расходиться в одном направлении, а при значении Е чуть больше – в противоположном направлении.
Поможем написать любую работу на аналогичную тему