Аналитическое решение

Проведем качественный анализ решений уравнения Шредингера применительно к рассматриваемой задаче.

Уравнения (1.1) в случае одномерного пространства запишется в виде:

По условию задачи (бесконечно высокие «стенки»), частица не проникает за пределы «ямы», поэтому вероятность ее обнаружения (а следовательно, и волновая функция) за пределами «ямы» равна нулю. На границах «ямы» (при х = 0 и х = l) непрерывная волновая функция также должна обращаться в ноль. Следовательно, граничные условия в данном случае имеют вид:

В пределах «ямы»  уравнение Шредингера (5.1) сведется к уравнению:

или

где

Общее решение дифференциального уравнения (5.4) имеет вид:

Так как по (5.2) , то B=0. Тогда:

Условие  выполняется только при , где n – целые числа, т.е. необходимо, чтобы

Из выражений (5.5) и (5.8) следует, что

т. е. стационарное уравнение Шредингера, описывающее движение частицы в «потенциальной яме» с бесконечно высокими «стенками», удовлетворяется только при собственных значениях , зависящих от целого числа n. Следовательно, энергия  частицы принимает лишь определенные дискретные значения. Таким образом, микрочастица в «потенциальной яме» может находиться только на определенном энергетическом уровне , или, как говорят, находиться в квантовом состоянии n.

Подставив в (5.7) значение k из (5.8) найдем собственные функции:

Постоянную. интегрирования A определим из условия нормировки (5.4), которая в данном случае запишется в виде:

В результате интегрирования получим , а собственные волновые функции будут иметь вид:

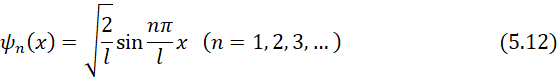
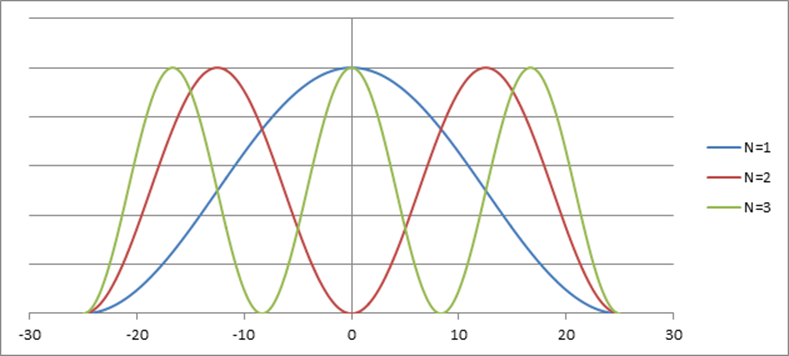
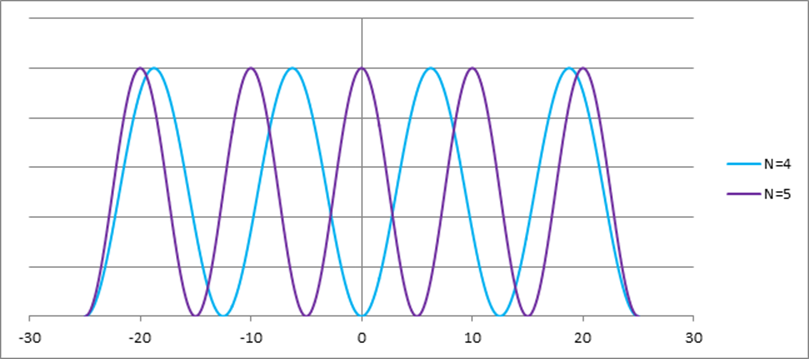
Графики собственных функций (5.12), соответствующие уровням энергии (5.9) при n = 1, 2, 3, 4 и 5, имеют тот же вид (см. Рис. 3), что и полученные при численном решении поставленной задачи. На Рис. 4 и Рис. 5 изображена плотность вероятности обнаружения частицы на различных расстояниях от «стенок» ямы, равная  для n = 1, 2 и 3 (см Рис. 4) и для n = 4 и 5 (см. Рис. 5).