Построение перпендикулярных прямых

Задача. Через данную точку О провести прямую, перпендикулярную данной прямой а.

Решение. Возможны два случая:1) точка О лежит на прямой а; 2) точка О не лежит на прямой а.

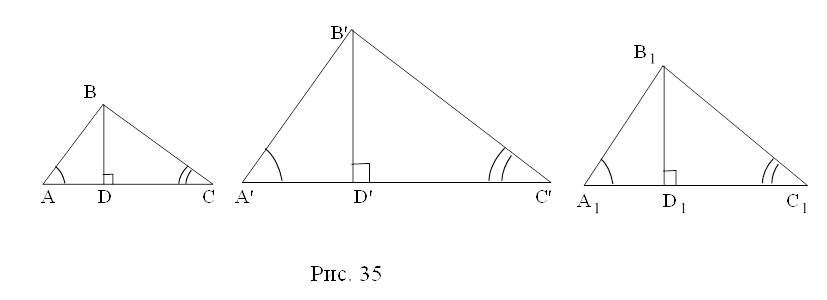
Рассмотрим первый случай (рис. 5). Из точки О проводим произвольным радиусом окружность. Она пересекает рямую а в двух точках: А и В. из точек А и В проводим окружности радиусом АВ. Пусть С – точка их пересечения. Искомая прямая проходит через точки О и С.

Перпендикулярность прямых ОС и АВ следует из равенства углов при вершине О треугольников АСО и ВСО. Эти треугольники равны по третьему признаку равенства треугольников.    

Рассмотрим построение и доказательство

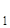
для второго случая (рис. 6).                                

Из точки О проводим окружность, пересекающую прямую а. Пусть А и В – точки ее пересечения с прямой а. Из точек А и В тем же радиусом проводим окружности. Пусть О – точка их пересечения, лежащая в полуплоскости, отличной от той, в которой лежит точка О. Искомая прямая проходит через точки О и О. Докажем это.

          Обозначим через С точку пересечения прямых АВ и ОО. Треугольники АОВ и АОВ равны по третьему признаку. Поэтому угол ОАС равен углу ОАС. А тогда треугольники ОАС и ОАС равны по первому признаку. Значит, их углы АСО и АСО равны. А так как они смежные, то они прямые. Таким образом, ОС – перпендикуляр, опущенный из точки О на прямую а.                                     

Построение треугольника по трем элементам

Задача 1.  Построить треугольник по двум сторонам и углу между ними.

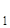Решение. Прежде всего уточним, как нужно понимать эту задачу, т. е. что здесь дано и что нужно построить. Даны отрезки РQ, РQ и угол hk (рис. 7а). Требуется с помощью циркуля и линейки (без масштабных делений) построить такой треугольник АВС, у которого две стороны, скажем АВ и АС, равны данным отрезкам РQ и РQ, а угол А между этими сторонами равен данному углу hk.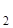

Проведем прямую а и на ней с помощью циркуля отложим отрезок АВ, равный отрезку РQ (рис. 7б). Затем построим угол ВАМ, равный данному углу hk. На луче АМ отложим отрезок АС, равный отрезку РQ, и проведем отрезок ВС. Треугольник АВС – искомый.

В самом деле, по построению АВ= РQ, АС= РQ, А=hk. описанный ход построения показывает, что при любых данных отрезках РQ, РQ и неразвернутом угле hk искомый треугольник построить можно. Так как прямую а и точку А на ней можно выбрать произвольно, то существует бесконечно много треугольников удовлетворяющих условиям задачи. Все эти треугольники равны друг другу (по первому признаку равенства треугольников), поэтому принято говорить , что данная задача имеет единственное решение.

Задача 2. Построить треугольник по стороне и двум прилежащим к ней углам.

Решение. Дан отрезок КМ и углы mp и rs (рис.8а). Требуется с помощью циркуля и линейки построить такой треугольник АВС, у которого сторона АВ, равна отрезку КМ, а углы А и В равны соответственно углам mp и rs.

Проведем прямую а и на ней с помощью циркуля отложим отрезок АВ, равный отрезку КМ (рис. 8б). Затем построим угол ВАN, равный данному углу mp. Построим угол АВН равный углу rs. Обозначим точку пересечения АN и BH как С. Треугольник АВС – искомый.

В самом деле, по построению КМ=АВ, ВАN=mp, АВН=rs.

Описанный ход построения показывает, что при любом данном отрезке КМ и условии mp+rs<180º  данный треугольник построить можно. Так как прямую а и точку А на ней можно выбрать произвольно, то существует бесконечно много треугольников, удовлетворяющих условиям задачи. Все эти треугольники раны друг другу (по второму признаку равенства треугольников), поэтому принято говорить, что данная задача имеет единственное решение.

Задача 3. построить треугольник по трем сторонам.

Решение. Пусть даны отрезки РQ, РQ и PQ (рис. 9а). Требуется построить треугольник АВС, в котором АВ= РQ, ВС= РQ,  СА= PQ.

Проведем прямую и на ней с помощью циркуля отложим отрезок АВ, равный отрезку РQ (рис. 9б). Затем построим две окружности: одну – с центром А и радиусом PQ, а другую – с центром В и радиусом PQ. Пусть точка С – одна из точек пересечения двух окружностей. Проведя отрезки АС и ВС, получим искомый треугольник АВС. В самом деле, по построению АВ=PQ, ВС= РQ, СА= PQ, т.е. стороны треугольника АВС равны данным отрезкам.

Задача 3 не всегда имеет решение. Действительно, во всяком треугольнике сумма любых двух сторон больше третьей стороны, поэтому если какой-нибудь из данных отрезков больше или равен сумме двух других, то нельзя построить треугольник, стороны которого равнялись бы данным отрезкам.