Оценка качества регрессионной модели. Способы улучшения качества регрессионной модели.

Качеством модели регрессии называется адекватность построенной модели исходным (наблюдаемым) данным. Для оценки качества модели регрессии используются специальные показатели:

1) парной линейный коэффициент корреляции, который рассчитывается по формуле:

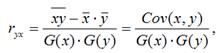
где G(x) – среднеквадратическое отклонение независимой переменной; G(y) – среднеквадратическое отклонение зависимой переменной. Также парный линейный коэффициент корреляции можно рассчитать через МНК-оценку коэффициента модели регрессии по формуле:

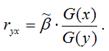
Парный линейный коэффициент корреляции характеризует степень тесноты связи между исследуемыми переменными. Он рассчитывается только для количественных переменных. Чем ближе модуль значения коэффициента корреляции к единице, тем более тесной является связь между исследуемыми переменными. Данный коэффициент изменяется в пределах . Если значение коэффициента корреляции находится в пределах от нуля до единицы, то связь между переменными прямая, т. е. с увеличением независимой переменной увеличивается и зависимая переменная, и наборот. Если коэффициент корреляции находится в пределах от минус еиницы до нуля, то связь между переменными обратная, т. е. с увеличением независимой переменной уменьшается зависимая переменная, и наоборот. Если коэффициент корреляции равен нулю, то связь между переменными отсутствует. Если коэффициент корреляции равен единице или минус единице, то связь между переменными существует функциональная связь, т. е. изменения независимой и зависимой переменных полностью соответствуют друг другу.

2) коэффициент детерминации рассчитывается как квадрат парного линейного коэффициента корреляции и обозначается как ryx2. Данный коэффициент характеризует в процентном отношении вариацию зависимой переменной, объяснённой вариацией независимой переменной, в общем объёме вариации.

Качество линейной модели множественной регрессии характеризуется с помощью показателей, построенных на основе теоремы о разложении дисперсий. Теорема. Общая дисперсия зависимой переменной может быть разложена на объяснённую и необъяснённую построенной моделью регрессии дисперсии.

В настоящее время существует две основных концепции в борьбе за повышение качества прогнозных регрессионных моделей:

− выявление с последующим исключением из анализа единственной аномальной невязки (выявление с последующим устранением нескольких аномальных невязок на основе  поэтапного устранения по одному выбросу);

− нахождение с последующим исключением большего количества невязок, которые не всегда являются аномальными и их совместное отбрасывание приводит к минимальным изменениям параметров исходного регрессионного уравнения.

Первую концепцию реализуют методы Эктона, Титьена-Мура-Бекмана, а так же Прескотта-Лунда. Эти методы предназначены для выявления с последующим удалением единственного аномального измерения при нормальном законе распределения случайных величин невязок и их количестве n ≥ 30.

Вторая концепция - первый метод принципиально новой концепции − метод Кука.  Несколько позднее появились методы Белсли-Ку-Уэлша и Аткинсона. Сущность метода Кука заключается в нахождении при отбрасывании уравнивающих измерений, которые стабилизируют параметры, нового регрессионного уравнения по отношению к исходному.