Расчет работы и эксергии тепла в замкнутых процессах с помощью e-i диаграммы.

Анализ необходимо начать с рассмотрения характеристик цикла Карно, занимающего особое положение среди всех циклов взаимного преобразования тепла и работы.  Рассмотрим его в приложении к реальному рабочему телу.

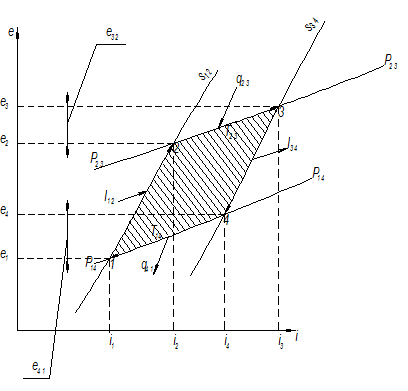
Рис.5.1. Цикл Карно в области насыщенного пара

На рисунке представлен прямой цикл в e-i диаграмме (все температуры выше T0). Процессы 1-2 и 3-4 представляют собой изоэнтропы, первая из которых связана с подводом работы (l1-2), приводящим к повышению давления от Р1 до Р2 и эксергии от e1 до e2, а вторая – с отводом работы (l3-4), которая вызывает понижение давления с  P3 =Р2  до Р4=Р1, и эксергии от е3  до  е4.

Процессы 2-3 и 4-1 изотермо-изобары, связанные с подводом (q23) и отводом (q41) тепла.

Эксергетический баланс цикла:

                                 l1-2 + q2-3 τe(2-3)= l3-4 + q4-1 τe(4-1)

или

                                 l3-4 - l1-2 = eq(2-3) – eq(4-1)

Отсюда следует, что работа цикла l = l3-4 - l1-2 равна разности эксергий eq подведенного и отведенного в цикле тепла. Поскольку величины эксергии тепла в цикле для изобарного процесса равны разности эксергий потока ((Δe)p=eq ), то выражение для разности работ в цикле можно представить так:

l = (е3 - е2) - (е4 - е1) = Δе3-2 – Δе4-1

         Пользуясь данным уравнением, можно определить величины eq в процессах 2-3 и 4-1, а также работу цикла по соответствующим отрезкам  на е-i диаграмме.

В обратном цикле Карно изменяются только знаки величин q и e. Способ определения характеристик цикла остается неизменным.

Цикл Карно как прямой, так и обратный может быть в реализован и в области газового состояния. Однако в этом случае изотермические процессы подвода и отвода тепла не могут вестись по изобарам, как в области влажного пара. Изотермический процесс подвода и отвода тепла должен сопровождаться понижением давления и отдачей внешней работы; процесс отвода тепла – повышением давления и подводом работы.

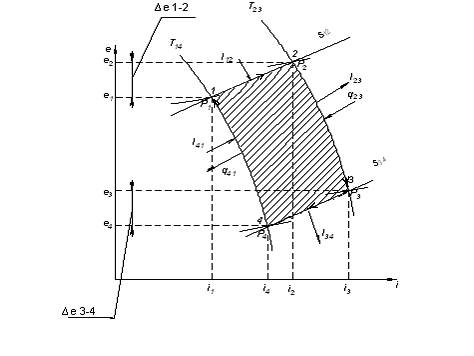
Рис. 5.2. Цикл Карно в области  газа

 Цикл представляется следующим образом: Процессы 1-2 и 3 -4  представляют собой изоэнтропы, а 2-3 и 4-1 – изотермы.

Так же как в предыдущем случае, величина работы в процессах 1-2 и 3-4  могут быть сняты непосредственно с диаграммы:

  l1-2 = Δе1-2 = Δi1-2 ;        l2-3 = Δе2-3 = Δi2-3

Значения работы и тепла в процессах 2-3 и 4-1 могут быть так же найдены по значениям Δе с учетом формул:

и

Эксергетический баланс процесса в этом случае:

                               l1-2+ l4-1 + eq(2-3)  = l2-3+ l3-4 + eq(4-1)

Работа цикла:

l = l2-3 +l3-4 – (l1-2+l4-1) = eq(2-3) - eq(4-1)

или

l= q2-3 τe(2-3) - q4-1 τe(4-1)

Если рабочее тело - идеальный газ, то значения тепла и работы в каждом изотермическом процессе равны:

l2-3 = q2-3;   l4-1 = q4-1

Из этого следует, что l1-2 = l3-4, т.к. суммарный баланс энергии для каждой изотермы и их суммы равен нулю:

(q2-3 – l2-3)+(l4-1 – q4-1)=0

Преобразование тепла в работу в таком цикле совершается только за счет разницы в величинах изотермических работ  l2-3 и l4-1. В прямом цикле l2-3>l4-1 и соответственно                                                                         q2-3>q4-1;  в обратном - l2-3<l4-1  и соответственно q2-3<q4-1.

 С аналогичных позиций могут быть проанализированы посредством e-i диаграммы «обобщенные циклы Карно», состоящие из 2-х изотерм и  двух связывающих их эквидистантных процессов. (чаще всего изобар или изохор)

Поскольку изобары и изохоры отличаются от изотерм, их проведение связано с  подводом и отводом тепла, которое осуществляется посредством регенеративного теплообменника.

Рассмотрим в качестве примера обратный цикл Стирлинга.

Он состоит из 2-х изохор и 2-х  изотерм.

Энергетический баланс цикла

l1-2+ q3-4 = q1-2 + l3-4

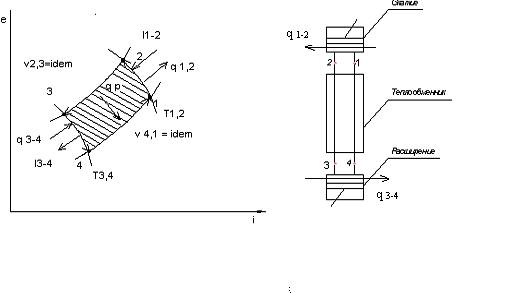
Рис.5.3.Обратный цикл Стирлинга в координатах е,i и его схема

Поскольку основным назначением цикла является не производство работы, а отвод тепла q3-4 на уровне T3-4 от охлаждаемого объекта, энергетический баланс удобно представить в виде:

                                      q3-4 = l3-4 - l1-2+q1-2 = l + q1-2

Эксергетический баланс цикла:

l1-2 + q3-4τe(3-4) = l3-4 + q1-2  τe(1-2)

Учитывая, что для холодильного цикла Т3-4<T0, а Т1-2=Т0, получим:

                                         l1-2 + eq(3-4) = l3-4

                                         eq(3-4) = l3-4 – l1-2 = l

Отведенная в виде холодопроизводительности полезная эксергия теплового потока q3-4, равная eq(3-4), равна затраченной в цикле работе l.

В цикле теплового насоса напротив T3-4 = T, а T1-2>T0.

Тогда аналогично:

eq(1-2) = l

Условием идеального цикла является отсутствие потерь эксергии во всех процессах, в том числе и при внутреннем теплообмене, связанном с передачей тепла в регенеративном теплообменнике от охлаждаемого потока. (процесса 2-3) к нагревающемуся (4-1). Это условие может быть выполнено только при соблюдении равенства:

                                              е2 – е3 = е4 – е1

                                              Δe2-3 =  Δe4-1, т.е.

увеличение эксергии нагревающегося потока Δe4-1 должно быть равно уменьшению эксергии охлаждаемого потока. Это условие имеет общее значение и применимо ко всем регенеративным обратимым процессам.