Определение КПД основано на уравнениях:
и 
.
Независимо от вида системы и характеристики происходящего в ней процесса, величина АЭ и АЗ качественно однородны.
Величина АЭ – приведенная производительность
АЭ = ΣEэ- включает все потоки эксергии, которые определяют полученный эффект,
AЗ = ΣЕз – определяет затраты.
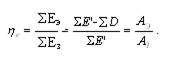
Для идеального процесса (ΣD = 0) 
Если вся подведенная эксергия расходуется или теряется ΣЕ′ = ΣD; 
Для реальных технических систем:
Чем выше 
, тем техническая система более совершенна.
Рассмотрим определение для тех же систем.
Теплосиловая установка
Полезный эффект ТСУ – АЭ = L
Затраты АЗ = E′q = 
КПД 
Из уравнения эксергетического баланса ТСУ
E′q = L + D, откуда L = E′q – D
Подставив выражение для L в формулу
, получили < 1
Величина показывает, какая часть введенной с тепловым потоком Q′ эксергии тепла перешла в работу L.
Сравним величину с термическим КПД 
. Определив из выражения для величину L=
и подставив его в выражение для 
, получим 
Таким образом, термический КПД представляет собой функцию двух переменных – эксерегтического КПД, отражающего степень термодинамического совершенства, и эксерегтической температуры.
Так как <1, а 
, значения 
всегда меньше единицы даже для идеальной машины.
Значит, характеризует эффективность работы системы косвенно.
Холодильная установка
Аэ = Е′q – приведенная холодопроизводительность;
Аз = L – подведенная эксергия (работа).
Тепловой поток Q", отведённый при T0 в окружающую среду, в баланс не входит, поэтому L=E′q+D
Таким образом, <1
Связь между и холодильным коэффициентом представляется в виде
;
Для ХМ ≤ 1, а 0 < τе < - ∞, поэтому холодильный коэффициент может быть как больше, так и меньше единицы. Он не связан непосредственно с совершенством установки и может быть большим у менее термодинамически совершенной системы. Эксергетический КПД характеризует совершенство однозначно, независимо от температурных условий.
Теплонасосная установка
Аэ = Е"q=Q" 
- отводимый тепловой поток;
Аз = L – подведённая эксергия.
Для ТН при T>T0, Q′ = 0 в баланс не входит, поэтому L=E"q+D
.
Таким образом, <1.
Связь между тепловым коэффициентом μ , ζ и можно установить сопоставлением формул для η = μ и ηе:
для механического привода
;
для теплового привода ζ = ηе τе′ / τе′′.
Для разомкнутых процессов подсчет эксергетического КПД производится так же, как и для рассмотренных циклов.
Определение КПД процесса теплообмена по первому началу термодинамики приводит к значению 
>1 при T < T0. Это противоречие устраняется при оценке эффективности эксергетическим КПД:
Аэ = Q"τ" – полезный эффект;
Аз = Q′τ′ - затраты.
Для изобарного процесса Q τе = ΔE, следовательно,
Теплообмен с окружающей средой при любом соотношении T и T0 приводит к уменьшению 
. Поэтому 
всегда меньше 1.
При термодинамическом анализе и оптимизации существенное значение имеет связь общих показателей системы с характеристиками её отдельных элементов. В общем виде, если обозначить некоторую эксергетическую характеристику, связанную с эффективностью системы в целом через Xe, через хеi такую же характеристику i – го элемента системы, то величина
zi = ∂ Xe /∂ хеi
будет показывать влияние изменений в отдельном элементе на характеристику системы в целом.
Коэффициент zi характеризует внутренние связи системы и определяется её структурой.
Для более простых систем КПД могут быть получены на основе аналитических зависимостей.
На практике достаточно часто встречаются системы с последовательно расположенными участками, процесс в которых протекает без отвода и подвода эксергии извне к отдельным элементам и без циркуляции её между элементами. В этом случае эксергия на выходе из i-ого элемента E”i всегда равна эксергии на входе в (i+1)-ый элемент E’(i+1). Поэтому
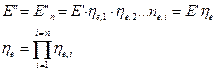
В системах без промежуточных подводов и отводов эксергиии эксергетический КПД системы равен произведению КПД всех входящих в него коэффициентов.
Поможем написать любую работу на аналогичную тему