Сжатие жидкостей и газов.

Сжатие рабочего тела в технических системах может происходить в различных температурных условиях:

1.Сжатие газа от начальной температуры, равной или близкой к T0. В этих  условиях τе. Процесс характерен для химических технологий.

2.В паровых холодильных машинах сжатие производится от температуры ниже T0 и в конце процесса может не достигнуть T0 или переходит в область T>T0. Поэтому τе может быть как больше, так и меньше нуля.

3.При сжатии горячих газов температура в течение всего процесса выше T0  и τе>0.

4.В низкотемпературных (криогенных) установках весь процесс сжатия протекает при температурах, значительно более низких, чем T0. Здесь τе<0.

Для всех процессов сжатия, независимо от условия их проведения действительно уравнение эксергетического  баланса:

Работа l, затраченная в компрессоре или насосе, расходуется на повышение эксергии рабочего тела , на тепло (отвод от газа или подводимое к нему), эксергия которого равна , и частично теряется на потери . Если процесс обратим

 Рассмотрим первый случай (τе):

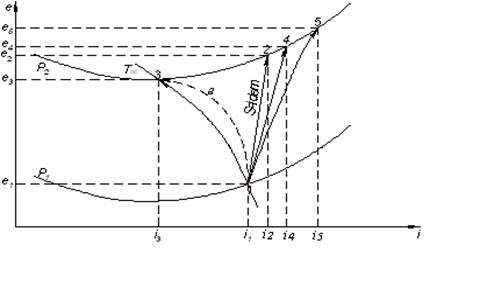
Рис.10.1. Процессы сжатия при τе (Т≥Т0 )

1-3 – обратимый изотермический процесс, температура остается постоянной, равной Т0. Эксергия eq, отводимая от газа в окружающую среду, eq = 0, т.к τе = 0

В необратимом изотермическом процессе температура газа отличается от Т0 в течение процесса. Но в начале и конце процесса температура равна Т0 (соблюдение конечных параметров). Следовательно, eq = 0.

Поэтому для изотермического процесса уравнение в общем случае получает вид:

                                      lиз = Δе3-1 + Σd

В частности, когда процесс обратим,  Σd = 0 и , следовательно,

                                      lиз = Δе3-1

Таким образом, величина работы lиз обратимого изотермического процесса может быть без вычислений снята с i-e диаграммы рабочего тела, как разность значений эксергии в начальной и конечной точках процесса.

Определив расчетным или опытным путем действительную работу l изотермического одноступенчатого компрессора, можно по величине Δе3-1, подсчитать его изотермический КПД, равный 

         Величина потерь от необратимости определяется по следующей формуле:

                                   Σd = l - Δе3-1

Эксергетическая диаграмма потоков для охлаждаемого изотермического компрессора имеет вид:

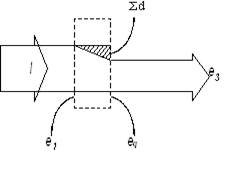Рис.10.2. Эксергетическая диаграмма потоков охлаждаемого компрессора

 Величины е1 = 0, еq = 0  показаны условно линиями со стрелками.

При адиабатном сжатии баланс эксергии аналогичен балансу при изотермическом сжатии. В обратимом адиабатическом процессе теплообмен с окружающей средой отсутствует. Поэтому уравнение

                                l = Δe + eq + ∑d = Δe + qe + ∑d

сохраняет вид.

Обратимое адиабатное сжатие изображается на рисунке прямой 1-4, идущей по линии s=const. Величина минимальной работы равна  Δe1-4 = Δi1-4

На диаграмме видно, что Δe41 > Δe31. Превышение адиабатической работы над изотермической равно Δe3-4.   

В реальном адиабатическом процессе часть работы компрессора затрачивается на трение и переходит в тепло, которое передается газу. Поэтому эксергия газа в конце процесса возрастает (точка 5). Однако, величина Δe5-3 не равна работе реального адиабатного процесса, а соответствует суммарной эксергии, которую нужно подвести к газу в виде  работы и эксергии тепла, чтобы провести процесс 1-5 обратимо.

Действительная работа  адиабатного процесса  Δi5-1 больше, чем Δe5-1, т.к. тепло, сообщаемое газу, получается за счет работы, что ведет к потере эксергии.

Процесс сжатия 1-2 занимает промежуточное положение между изотермой и изоэнтропой и в отличие от процесса 1-5 проходит с отводом тепла.

Работа реального процесса 1-2 не может быть снята с  диаграммы, так же как и работа, нужная для проведения любого необратимого процесса, за исключением адиабатного, когда δq = 0. 

  Количество затраченной работы при одном и том же начальном и конечном состояниях может быть больше или меньше: соответственно  изменится  только отвод тепла в окружающую среду.

Второй случай (τе ><):

 Различные процессы сжатия показаны в е-i диаграмме.

Рис.10.3. Процессы сжатия при τе ><

1-3 -адиабатическое сжатие;

1-4 -процесс сжатия, идущий при температуре T<T0;

4-3-процесс сжатия при температуре выше окружающей среды (τе > ).

Величина работы, необходимая для сжатия, равна Δe31

Так же как и в предыдущем случае, часть работы, затраченная на повышение температуры вещества на участке 4-3 бесполезно теряется, т.к.  для  дальнейшего процесса рабочее тело нужно будет снова охлаждать до Т0 (точка 5).

Поэтому более рационально вести процесс сжатия от точки 4 по изотерме 4-5. В этом случае будет сэкономлена работа Δe3-5. Общая затрата работы на сжатие в этом случае будет равна Δe5-1. Таким образом для второго случая, когда (τе ><) идеальным процессом сжатия будет адиабатное сжатие до точки Т0  и затем изотермическое  сжатие до конечного давления.

КПД процесса

                    , где

lд  зависит от характера ведения процесса.

Третий случай: (τе>0)

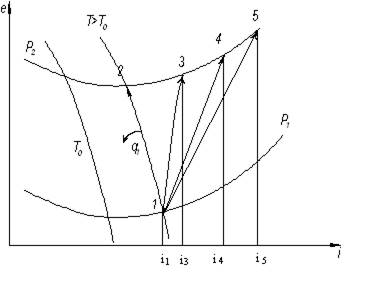
Рис.10.4. Процессы сжатия для условия   τе>0

 1-2 – процесс изотермического сжатия. Обратимая работа этого сжатия может быть найдена по величинам е1 и е2 и формуле               

Тепло q, отводимое от сжимаемого газа при T>T0, может быть использовано для получения работы, величина которой в идеальном случае составит eq = qτe. Эта работа может быть реализована с целью уменьшения затрат на сжатие. 

Общая минимальная работа,  необходимая для проведения идеального процесса 1-2, составит

                                          Δe2-1 = l - eq

          Адиабатный обратимый процесс сжатия изображен линией 1-4.

При этом минимальная работа сжатия Δe4-1 = Δi4-1 больше, чем Δe2-1.  

При необратимом адиабатном сжатии затрата работы l определяется  величиной     l = i5 – i1, а потеря

                                                d=i5 –i1 – Δe5-1

Эксергетический КПД для адиабатной ступени определяется как

Действительный процесс сжатия с охлаждением компрессора изображается линией 1-3. Работа этого реального процесса по диаграмме определена быть не может, т.к. сжатие необратимо и сопровождается отводом тепла.

Четвертый случай (τе<0).

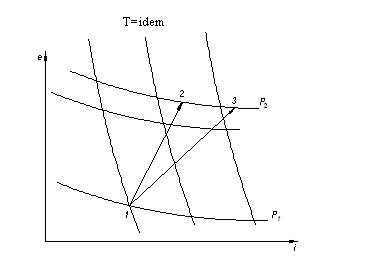
Рис. 10.5. Адиабатное сжатие при   τе<0

Приведённые на рис. 10.5. изотермы соответствуют температурам значительно более низким, чем Т0.

Для обеспечения процесса сжатия при Т0 необходимо наличие охлаждающего устройства для отвода тепла от рабочего тела при T<Т0 и передачи его в окружающую среду. Такое сжатие в компрессоре  с отводом  тепла при Т<T0 в низкотемпературной технике не применяется.

         Обратимое адиабатное сжатие соответствует линии 1-2 по изоэнтропе.

Реальный адиабатный процесс изображается линией 1-3.

 КПД процесса определяется по формуле

Все изложенные закономерности в равной степени относятся и к сжатию жидкостей.