Процессы расширения в низкотемпературных системах.

Общая черта всех процессов расширения в низкотемпературных системах – это преобразование эксергии давления ер в эксергию ет, связанную с охлаждением.

В зависимости от  способа расширения такое преобразование протекает по-разному. Оно может сопровождаться отводом энергии как в форме работы (адиабатный детандер), так и в форме тепла (неадиабатная вихревая труба); отводом энергии в виде работы с одновременным подводом энергии от охлаждаемого объекта в форме тепла (неадиабатный детандер); может вообще происходить без энергетического обмена (адиабатное дросселирование).

Эксергетический метод позволяет вывести единый для всех этих процессов КПД, позволяющий сравнивать их в сопоставимых условиях.

Эффектом всех процессов расширения является эффект охлаждения. В общем виде процесс расширения при низких температурах (Т<Toc,τе < 0) показан  на рис. 11.2 в координатах е-i.

Рабочее тело из состояния, соответствующего точке 1 и давлению р1, расширяется до точки 2 (давление р2); его температура снижается от Т1  до Т2.

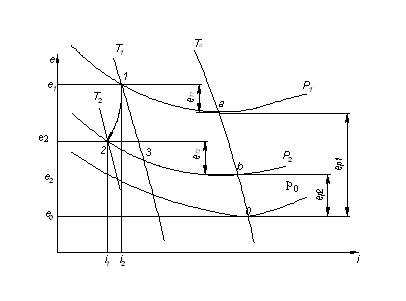
Рис.11.2. Обобщённый процесс расширения при Т<Toc

Эксергия рабочего тела уменьшалась от е1 = ет1 + ер1 до  е2 = ет2 + ер2

При этом величина ер уменьшается от ер1 до ер2 величина ет возрастает  от ет1 до ет2..  Такое превращение ер в ет  возможно потому, что в области Т<Toc изобары имеют наклон, противоположный тому, который характерен для высокотемпературной области.

          Эксергетический  КПД превращения  ер в ет составит:

                                         ηе  = ∆ет /    eр = (ет2  - ет1 )  / (  е р1   -  ер2)

     Преобразуем это уравнение к более удобному виду:

        ▼ eр = ер,1 - ер,2 = ▼еа,0 - ▼ еb,0   =  ▼еа,b

         ∆ет  = е Т,2    - еТ,1  =  ∆е2,b - ∆е1,а  =  ∆еа,b   - ∆е1,2 

Отсюда

                                  ηе  = (∆еа,b  - ∆е1,2 ) /  ▼еа,b

Практически для вычисления КПД  процессов расширения при Т<Toc целесообразно заменить величину ▼еа,b  близкой ей величиной▼е1,3 – разностью эксергий между заданными давлениями по изотерме Т1 вместо То.с.. В этом случае

                                 ηе   =  ∆е2,3  /  ▼е1,3

Дросселирование

В теплотехнике сравнительно небольшое нагревание газа при дросселировании не находит технического применения, т.к. такой эффект всегда может быть получен более простым путём.

В технике низких температур охлаждение, полученное при дросселировании, служит основой большинства низкотемпературных процессов.

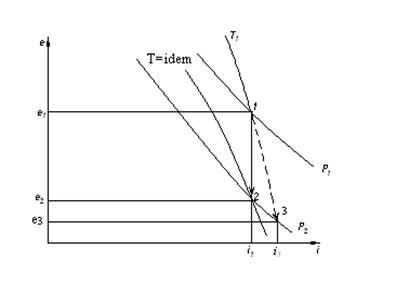
Рис.11.3. Процесс дросселирования в низкотемпературных системах, протекающий с охлаждением

На рисунке 11.3. изображен процесс дросселирования с охлаждением.

Точка 1 - начальное состояние при  Т1, Р1;

Точка 2 - конечное состояние  при Т2, Р2 .

При этом Т2<T1, прямая 1-2 – i = idem–процесс дросселирования.

Изменение эксергии при дросселировании определяется разностью её значений в начальной и конечной точках.

В процессе адиабатного дросселирования при отсутствии энергетического обмена работой тела с  окружающей средой величина е1-2  равна потере от необратимости

                                          е1-2 = е1 –е2 =d

Эксергетический КПД процесса дросселирования определяется величиной                         

                             ηе  = ∆е2-3  /  е1-3  ,

где т.3 определяется пересечением изотермы   Т1   с изобарой    р2.

Детандирование (расширение)  с отдачей внешней работы.

Адиабатный детандер.

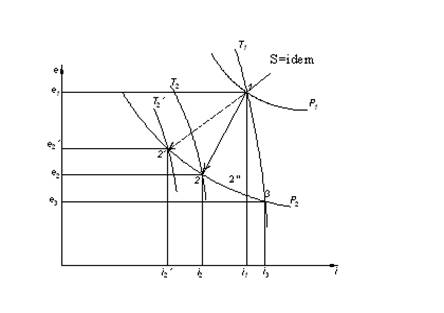
Рис.11.4. Расширение газа в адиабатном детандере

Линия   1-2′  соответствует адиабатному процессу расширения от давления Р1  до давления  Р2  при условии  S = idem.

Эффект охлаждения в этом предельном случае, выраженный в единицах эксергии, равен

                                   ∆е2,-3  = е2, – е3;  

в количестве тепла эффект охлаждения равен

                                    q = i2, - i3 .

 Отдаваемая работа равна l = i1 -   i2, .

Практически, из-за внутреннего теплообмена, трения, притока тепла извне и другим необратимым эффектам процесс в детандере протекает с увеличением энтропии и большим снижением эксергии, чем при    S = idem. При этом эффект охлаждения  и количество отдаваемой работы уменьшаются. Чем больше потери от необратимости, тем меньше и эффект охлаждения, и внешняя работа.  В пределе процесс сведётся к дросселированию

 Линия 1-3 соответствует изотермическому процессу расширения без какого либо эффекта охлаждения.  

Эксергетический КПД реального детандера:

Здесь - подведенная эксергия, которая расходуется на эффект охлаждения () и внешнюю работу (l=).

При условии  s = const =, числитель дроби  = и =1. В процессе 1-3 эффект охлаждения и внешняя работа равны нулю, поэтому =0

Неадиабатный детандер ( αi > 0)

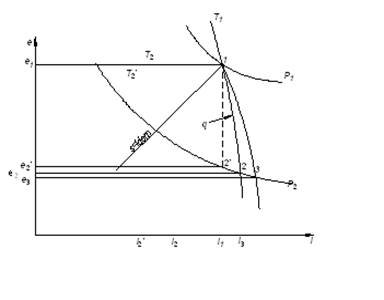
Рис.11.5.Расширение газа в неадиабатном детандере

Процесс расширения 1-2,   сопровождаемый подводом тепла q от охлаждаемого объекта, в зависимости от величины q может заканчиваться на любой точке изобары P2 между линиями  s==idem и T=idem.  При q =0 процесс совпадает  с линией s==idem (идеальный адиабатный детандер). При T=idem   величина q достигает наибольшего значения (идеальный изотермический детандер).

Эксергетический КПД такой машины определяется по формуле.

Внешняя работа l не равна , поскольку процесс неадиабатный. Поэтому величина l должна быть определена или измерением или по уравнению энергетического баланса     l = i1 – i2 + q