Разделение смесей в реальных установках всегда требует энергетических затрат, превышающих величину, найденную для идеального процесса из условий эксергетического баланса или по е – ξ диаграмме для бинарных смесей.
Значительное увеличение расхода энергии связано с различными потерями “d” от необратимости.
Рассмотрим определение потерь и КПД в процессах разделения бинарных смесей.
Общий вид схемы материального и энергетического баланса системы, в которой происходит процесс разделения, приведён на рис.13.1.
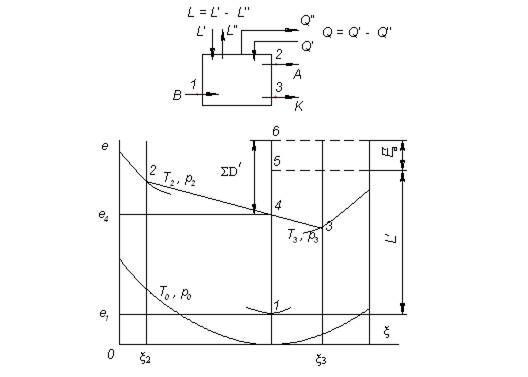
Рис.13.1. Схема материального и энергетического балансов процесса разделения бинарной смеси и изображение состояний продуктов на е – ξ диаграмме.
К системе подводится разделяемая смесь В при параметрах, соответствующих точке 1, и отводятся продукты разделения А и К, состояние которых характеризуется параметрами точек 2 и 3.
В общем случае для обеспечения работы системы к ней должно подводиться некоторое количество эксергии в виде тепла Q и работы L.
В зависимости от конкретных условий, количества тепла и работы могут иметь различные величины и знаки, но во всех случаях будут соблюдаться уравнения материального, энергетического и эксергетического балансов.
Материальный баланс
B = K + A
Bξ1 = K ξ3 + A ξ2![]()
Энергетический баланс
I1 + Q + L = I2 + I3
Bi1 + Q + L = Ai2 + Ki3
Эксергетический баланс
E1 + Eq + L = E2 + E3
Be1 + Eq + L = Ae2 + Ke3 + ΣD.
Последнее уравнение может быть наглядно интерпретировано на е – ξ диаграмме.
Точки, соответствующие состоянию смеси В и продуктов разделения А и К (1, 2, 3), нанесены на диаграмму с указанием температур, давлений, концентраций. Для общности эти параметры взяты различными.
Суммарная эксергия E'' = Ae2 + Ke3, отводимая с продуктами разделения, изображается ординатой точки 4.
Эксергия е1, подводимая с единичной массы смеси В, соответствует ординате точки 1. Так как в данном случае она меньше, чем отводимая, то процесс разделения без дополнительного подвода эксергии невозможен; необходимо подвести эксергию любого вида в количестве, не меньшем, чем Δе1 – 4 (отрезок 4 –1).
Практически, учитывая потери от необратимости, нужно подвести такое количество эксергии E'q + L', чтобы оно превышало отводимую эксергию е4 на величину ΣD/B = ΣD'. Чем больше величина е1, тем меньше нужно дополнительной эксергии.
Как уже указывалось, при достаточной величине проведение процесса может быть обеспечено только за счет эксергии продукта, подводимого для разделения. Обычно эта эксергия создается путем предварительного сжатия разделяемой смеси.
В рассматриваемом примере подводятся: L' (отрезок 5 – 1) и эксергия тепла Еq (отрезок 5 – 6). Следовательно, величина ΣD' в соответствии с эксергетическим балансом будет изображаться отрезком ординат е6 – е4.
Эксергетический КПД процесса разделения смеси:
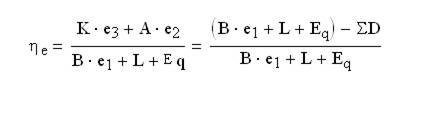
Рассмотрим, как применяется данный метод анализа к широко распространенному в химической технологии методу ректификации.
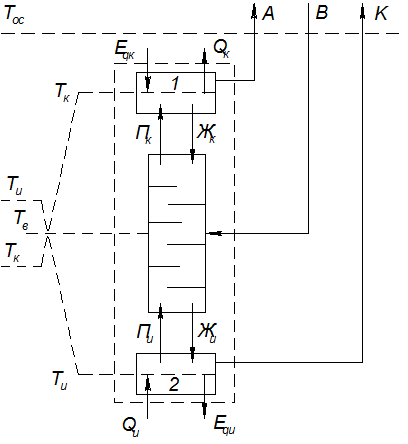
Рис.13.2. Схема ректификационной колонны
Для обеспечения работы любой ректификационной колонны, в частности низкотемпературной, необходимо:
1.Произвести отвод теплового потока Qк от конденсатора колонны на уровне Тк;
2.Подвести тепло к испарителю колонны на уровне Ти > Тк;
3.Подвести к колонне разделяемую смесь В и отвести продукты разделения А и К таким образом, чтобы посредством теплообмена между ними привести продукты разделения к температуре окружающей среды Тос, а разделяемую смесь – к температуре входа в колонну Тк < Тв < Тн.
Применительно к низкотемпературной ректификации все температуры, связанные с процессом, ниже Тос. В этих условиях процесс1 требует затраты эксергии Еqк, а процесс 2, напротив, дает возможность получить некоторую эксергию Еqн, которая при близких значениях Qк и Qн меньше Еqк по абсолютной величине, так как Тк < Тн, и, следовательно, │τeк│=│τeн│.
Обычно эти процессы проводятся совместно; разность Еqк – Еqн равна минимальной затрате работы, необходимой для обеспечения процесса разделения в колонне. Эта величина даже при отсутствии других потерь, больше, чем обратимая работа разделения.
Как известно, обратимое действие ректификационной колонны возможно лишь при условии, что тепло отводится в каждом сечении колонны выше ввода и подводится в каждом сечении ниже ввода разделяемой смеси В. Только в этом случае может быть обеспечено такое изменение количества потока жидкости Ж и пара П по колонне, которое необходимо для обратимого тепло- и массообмена. В колонне (адиабатной), показанной на рисунке, это требование не выполняется, так как тепло отводится только в конденсаторе (Qк) и подводится только в испарителе (Qи).
Таким образом, первое отклонение от идеального процесса, приводящее к потерям от необратимости, связано с адиабатным протеканием процесса в колонне. Обозначим потери, связанные с этим отклонением, через D1.
Вторым фактором, приводящим к потерям при ректификации, являются конечные разности температур в конденсаторе и испарителе при отводе и подводе тепловых потоков Qк и Qи .Обозначим эти потери через D2.
Расход работы на отвод тепла Qк и подвод Qи будет в реальных условиях больше, чем разность Еqк – Еqн, так как оба процесса осуществляются с потерями. Обозначим эти потери через D3.
Процессы теплообмена между поступающей смесью В и отходящими продуктами разделения А и К также приводят к потерям D4.
Кроме того, необходимо учесть потери D5, связанные с притоком тепла через изоляцию.
Потеря D2 в отличие от D1 является целиком технической и может быть снижена путём уменьшения ∆Т. Это достигается увеличением поверхности теплообмена или скорости потока.
В технических системах разделения существенную роль играют как потери D3 и D4 , так и другие, связанные с особенностями их схем и конструкций.
После вычисления перечисленных потерь эксергии КПД колонны определяется по приведённой выше формуле.
Поможем написать любую работу на аналогичную тему

