Задача эксергетической технико-экономической оптимизации сводится к определению параметров технической системы, минимизирующих в заданных условиях функционалы:
З = (ΣSэн + ΣSнэн)/ρ′′e ( ЭТЭ – метод)
Зе = qтек + qк (СУЗ ЭКС – метод)
Общее направление ЭТЭ оптимизации независимо от вида целевой функции определяется двумя основными инженерными задачами:
1. Оптимальное проектирование технических систем, включающее выбор оптимальных технологических схем (структуры), а также технологических и конструктивных параметров оборудования.
2. Оптимизация действующих технических систем путем изменения технологических параметров и конструктивных параметров оборудования при неизменной схеме (структуре).
На практике могут встречаться различные сочетания этих задач. Множество возможных постановок задач при ЭТЭ оптимизации наиболее удобно представить в виде классификатора.
Основной признак деления на классы 1 и 2 задач ЭТЭ оптимизации – это заданность структуры или возможность ее свободного выбора при постановке задачи. Вводятся понятия: простая система, сложная система.
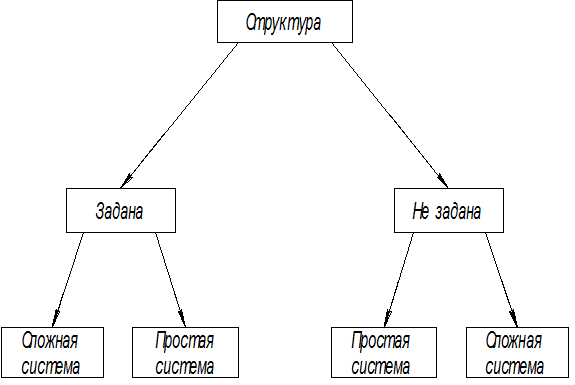
Рис.18.1.Классификация возможных постановок задач ЭТЭ оптимизации преобразования энергии и вещества
Простая система – система, для которой может быть установлена аналитическая зависимость (на основе математического моделирования или предварительного экспериментального исследования) между целевой функцией и исследуемыми параметрами.
Сложная система – система, для которой установить аналитическую зависимость нельзя.
Независимо от сложности систем к их оптимизации, как было видно ранее, можно подойти двояко.
Можно, разделив термодинамическую и технико-экономические части, решить задачу последовательно. Вначале, используя как целевую функцию ηе, найти относительно узкую область значений исходных параметров, где система имеет наибольший КПД. Затем, на втором этапе, производится сопоставление по капитальным (или приведенным) затратам и окончательно выбирается наилучший вариант. Такой подход при слабой корреляции капитальных и эксплуатационных затрат может дать хорошие результаты.
Можно решить задачу, одновременно рассматривая как термодинамическую, так и технико-экономическую часть. Для этого используется любая из соответствующих целевых функций ЭТЭ , СУСЭКС или для надежности обе.
Для решения оптимизационной задачи необходимо также, по возможности, ограничить область вариации исходных параметров.
Для этого существует три подхода – структурный, вариантный и их сочетание структурно-вариантный.
При структурном подходе предполагается, что влияние каждого из варьируемых параметров на целевую функцию известно. Следовательно, становится возможным сократить область вариации исходных параметров при выходе на экстремум. Это делается либо путем применения соответствующих математических методов при знании аналитических зависимостей между целевой функцией и параметрами, либо из физических соображений при условии предварительного экспериментального изучения влияющих параметров на целевую функцию.
Эти пути решения задачи в любом случае должны пройти через выявление наиболее влиятельных с технико-экономической точки зрения оптимизирующих факторов.
Варьирование этих уже немногих факторов позволяет относительно легко найти оптимальное решение.
При вариантном подходе необходим направленный или “слепой” перебор величин варьируемых параметров в пределах, определяемых из предварительных соображений, с целью нахождения их оптимальных значений.
При структурно-вариантном подходе в первую очередь производится перебор варьируемых параметров тех элементов системы, устранение потерь в которых приводит к максимальному увеличению термодинамической эффективности системы. Тем самым по сравнению с вариантным подходом сокращается число варьируемых параметров и соответственно область их варьирования.
Выбор того или иного подхода определяется структурой системы и способом решения: последовательным – сначала оптимизация по ηе, затем по приведённым затратам; или одновременным – по целевым ЭТЭ и СУЗ ЭКС функциям.
Примером оптимизации по ЭТЭ целевой функции З служат работы, посвященные оптимизации холодильных установок. При этом оптимизируемая система подвергается декомпозиции, посредством которой она представляется как ряд зон, в каждой из которых определяется стоимость потоков эксергии. Затем с помощью метода неопределенных множителей Лагранжа определяется глобальный экстремум. Для этого должна быть составлена и решена соответствующая система дифференциальных уравнений (уравнений Эйлера). Схема процесса комплексного разделения воздуха представлена на рисунке 18.2.
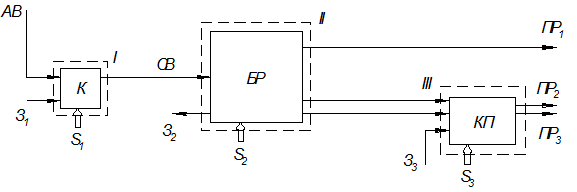 Рис.18.2. Схема разделения на зоны установки разделения воздуха
Рис.18.2. Схема разделения на зоны установки разделения воздуха
Зона I включает воздушный компрессор К с относящимся к нему оборудованием. В зону поступает атмосферный воздух, эксергия которого равна нулю, электроэнергия Э1 и соответствующие затраты S1. Продукцией зоны является сжатый воздух, служащий исходным продуктом зоны II. Зона II включает блок разделения воздуха БР. В этой зоне воздух разделяется на продукты ПР1, причем за счет расширения некоторой его части в сеть возвращается энергия Э2 < Э1. Затраты в этой зоне составляют величину S2. В третьей зоне два продукта разделения ПР2 и ПР3 сжимаются до давления, необходимого для потребителя. На сжатие расходуется электроэнергия Э3, связанные с этим процессом затраты имеют величину S3.
В каждой зоне могут быть выделены необходимые для более подробного анализа участки, например, в блоке разделения теплообменник (регенератор), разделительная колонна и т. д.
Для полного технико-экономического анализа необходимо знать все затраты, входящие в целевые функции З и Зе. На этой основе для каждой анализируемой системы составляется расчетная схема соответствующих балансов. В качестве примера приводится такая схема для систем из трех последовательно расположенных зон.
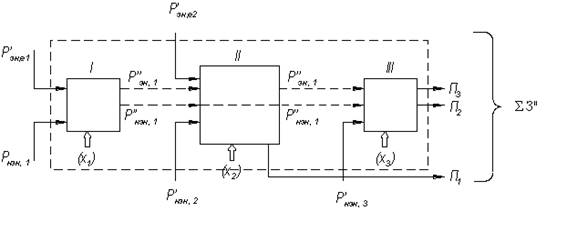
Рис.18.3. Схема баланса затрат системы, состоящей из трёх зон
Ввод энергетических затрат производится только в зоны I и II, получение конечных продуктов в зонах II (продукт П1) и III (два продукта – П2 и П3). Штриховыми линиями показаны внутренние стоимостные потоки, сплошными – внешние. Величины ее, i = Ее, i/ΣР′′е представляют собой удельные потоки внешней эксергии (вещества и энергии) в каждой зоне.
Тогда для рассматриваемой системы ΣЗ′′ для i-ой зоны составит
ΣЗ′′ = ΣРэн, ie, i + ΣРнэн, i = Рэн, e, i, 1 + Рэн, e, 2 + Рнэн, 1 + Рнэн, 2 + Рнэн, 3
Через х показаны варьируемые при оптимизации параметры в каждой зоне. Процесс оптимизации сводится к тому, что величины как внешних, так и внутренних потоков затрат, поступающих в каждую зону, выражают как функции величин, выходящих из этой зоны, и изменяемого параметра xi, представляющего собой независимые переменные. Эти операции производятся последовательно, по направлению от конца технологической цепочки к ее началу. Для самых простых случаев минимальное значение З можно найти алгебраическим путем.
В заключении можно отметить, что эксергетическая и технико-экономическая оптимизация систем преобразования энергии и вещества позволяет охватить более широкую информацию, чем чисто термодинамическая оптимизация ЭТЭ оптимизация позволяет учесть факторы, связанные с затратами на создание как самой системы, так и на обработку и доставку к ней материалов и энергии, т. е. всех эксергетических потоков.
Однако в современных условиях и такая оптимизация не всегда достаточна. Во многих случаях нужно учитывать экологические факторы, действие которых стало сопоставимо с происходящими на земле природными процессами.
Таким образом, необходима третья ступень оптимизации технических систем – технико – экономическая экологическая оптимизация. Для этого нужна оценка технико – экологического совершенства технических систем. Работа в этом направлении уже ведётся.
Поможем написать любую работу на аналогичную тему

