Случайная погрешность - это погрешность, изменяющаяся случайным образом при повторном определении одной и той же физической величины с помощью одной и той же измерительной аппаратуры при неизменных внешних условиях.
Случайные погрешности вызываются большим количеством факторов, воздействия которых столь незначительны, что их нельзя выделить и учесть в отдельности. Случайную погрешность можно рассматривать как суммарный эффект действия таких независимых факторов.
Случайные погрешности могут возникнуть из-за погрешности округления при отсчете показаний, нестабильности переходного сопротивления в контактах коммутирующих устройств, нестабильности напряжения источника питания, влияния электромагнитных полей и других влияющих величин. Основная их особенность - непредсказуемость. Но можно утверждать с определенной долей уверенности, что истинное значение измеряемой величины заключено в интервале от минимального до максимального результатов измерения.
Можно допустить, что и систематические, и случайные погрешности вызываются сигналами помехи, накладывающимися на тот сигнал, который должен быть измерен. Но если для систематической погрешности этот сигнал детерминированный, то для случайной погрешности он флуктуирует.
Случайную погрешность нельзя исключить в каждом из результатов измерений. Но с помощью многократных наблюдений, а также используя методы теории вероятности и математической статистики, можно учесть их влияние на оценку истинного значения измеряемой величины. Это позволяет определить значение измеряемой величины со значительно меньшей погрешностью, чем погрешности отдельных измерений (наблюдений).
На первый взгляд, случайные погрешности не подчиняются никакой закономерности. Но при анализе результатов измерений выясняется, что за кажущимся отсутствием какой-либо закономерности в чередовании погрешностей по знаку и по величине скрываются закономерности статистического характера, которые выявляются при массовых проявлениях погрешности. А именно:
- как бы ни был велик ряд погрешностей измерений, эти погрешности колеблются в определенных, достаточно узких, пределах;
- случайные погрешности встречаются и со знаком "плюс" и со знаком "минус" примерно одинаково часто;
- среднее арифметическое случайных погрешностей измерений одной и той же величины, произведенных в одинаковых условиях, стремится к нулю при неограниченном увеличении числа измерений;
- чем больше абсолютное значение погрешности, тем реже она встречается.
Для получения оценок характеристик случайных величин с наибольшей достоверностью они должны удовлетворять требованиям состоятельности, несмещенности и эффективности.
Состоятельность обеспечивается, если при бесконечном увеличении количества наблюдений оценка случайной величины стремится к истинному значению этой величины.
Несмещенность обеспечивается, если математическое ожидание оценки равно истинному значению случайной величины.
Эффективность означает, что дисперсия оценки минимальна.
На практике не всегда удается в полной мере обеспечить все эти требования, поэтому выбору оценки должен предшествовать критический анализ с точки зрения наилучшего удовлетворения указанным требованиям.
Необходимо отметить, что одна и та же влияющая величина может являться причиной появления как систематической, так и случайной погрешности. Так, при использовании для получения результата измерения стрелочного измерительного прибора причиной возникновения погрешности, в частности, является неправильность его градуировки. Если проводить измерения одним и тем же прибором, то погрешность результата измерения, обусловленная неправильной градуировкой, является систематической. Если же измерения производить различными измерительными приборами, выбираемыми из набора, произвольно взятого из некоторой партии приборов, то погрешность, обусловленная неправильностью градуировки, случайна, так как в этом случае случайным является сам выбор прибора.
Следует различать такие понятия, как точность результата измерения, точность измерительного устройства и точность процесса измерения. Эти понятия не тождественны, хотя и связаны между собой. Очевидно, что точность результата измерения зависит от точности измерительного устройства и точности процесса измерения, а для оценки точности средства измерения следует использовать точность результатов, получаемых с его помощью.
Одним из важнейших вопросов при рассмотрении случайных погрешностей является вопрос о количественной оценке степени доверия к результатам измерения. Для этого критерий, выражающий количественно оценку степени доверия, должен удовлетворять ряду требований:
1) должна иметься возможность выражения меры степени достоверности результата измерения в виде числа;
2) способы определения числового значения должны быть установлены так, чтобы при одинаковых условиях количественная оценка степени достоверности не зависела от субъективных особенностей оператора, а отражала объективную ситуацию;
3) критерий должен соответствовать интуитивному, основанному на опыте представлению о достоверности;
4) критерий должен обеспечивать возможность его практического применения.
Таким требованиям удовлетворяют принятые для оценки степени достоверности понятия доверительного интервала и доверительной вероятности. Доверительная вероятность - это вероятность того, что истинное значение измеряемой величины хи находится внутри доверительного интервала с границами D1 и D2:
(4.1)
Доверительный интервал - интервал, накрывающий с заданной доверительной вероятностью истинное значение измеряемой величины.
Оценить точность результата измерения - это найти доверительный интервал при заданной доверительной вероятности либо решить обратную задачу - найти доверительную вероятность при заданном доверительном интервале.
Наиболее полной характеристикой случайной величины является закон ее распределения. Различают две формы описания закона распределения: интегральную и дифференциальную. Интегральной функцией распределения называется функция F(x), каждое значение которой для каждого х является вероятностью события, заключающегося в том, что любая случайная величина хi окажется меньше некоторого значения х:
В метрологии принято использовать, в основном, дифференциальную форму – представление через закон распределения плотности вероятности случайной величины.
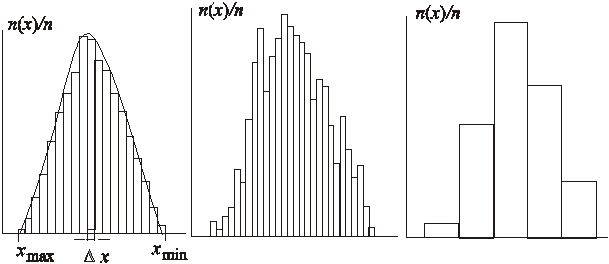
Дифференциальный закон распределения можно определить через построение гистограммы. Для этого необходимо произвести n независимых наблюдений. При этом каждое наблюдение, возможно, отличается от предыдущего, так как содержит случайную погрешность. Следует разбить интервал между наибольшим и наименьшим измеренными значениями на ряд равных интервалов шириной Dх. Подсчитывается количество наблюдений, попавших в каждый интервал (x, x + Dх). По результатам подсчетов строится график: на ось абсцисс наносятся значения результатов наблюдений и обозначаются границы интервалов, на ось ординат – относительная частота попаданий в интервал. В результате получим фигуру, состоящую из ряда прямоугольников с основанием, равным ширине интервала, и высотой, равной относительной частоте попаданий в каждый интервал (рис. 4.1а). Гистограмма – это диаграмма, полученная в результате нормализации. В такой диаграмме на ось ординат нанесены отношения количества попаданий в интервал n(х) на общее количество наблюдений n.
Если при этом ширину интервала выбрать слишком малой, то огибающая диаграммы будет сильно изрезанной (рис. 4.1б). При слишком большом значении ширины интервала огибающая диаграммы недостаточно четко выявит форму распределения (рис. 4.1в), поэтому существует правило для выбора размера интервалов:
а) б) в)
Рис. 4.1. Гистограммы: а - при правильном выборе ширины интервала Dх;
б - при слишком малых значениях Dх; в - при слишком больших значениях Dх
. (4.2)
Если n < 25, то значение Dх определяется по правилу Старжеса:
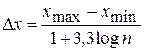. (4.3)
Если принять общую площадь, ограниченную контуром гистограммы и осью абсцисс, за единицу, то отношение площади соответствующего прямоугольника шириной (x, x + Dх) к общей площади равно относительной частоте попадания результатов наблюдений в тот или иной интервал. Если количество наблюдений растет, а диапазон xmax - xmin остается в ограниченных пределах, то число интервалов и, следовательно, число столбцов в гистограмме увеличивается при одновременном уменьшении ширины интервалов. При бесконечном уменьшении ширины интервала (x, x + Dх) ® 0 с одновременным увеличением количества наблюдений до бесконечности ступенчатая кривая, огибающая гистограмму, перейдет в плавную кривую, которая является кривой плотности распределения вероятности случайной величины (рис. 4.2). По определению
(4.4)
Данное выражение можно зависать в виде
(4.5)
Из последнего выражения и рис. 4.2 видно, что f(x)dx есть вероятность попадания результата наблюдения в интервал (x, x + dx). Проинтегрировав f(x)dx в интервале от плюс бесконечности до минус бесконечности, получаем результат, равный 1:
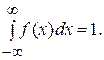
Равенство площади под плотностью распределения вероятностей единице означает, что любой результат наблюдения попадет в интервал от плюс бесконечности до минус бесконечности. Зная плотность распределения вероятностей, можно найти вероятность того, что результат очередного наблюдения x окажется равным или меньшим определенного значения а:
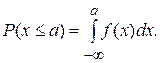
Эта величина равна площади под f(x) слева от линии а (рис. 4.2).
 |
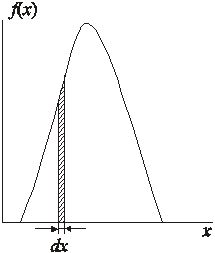Рис. 4.2. Плотность распределения вероятности
Математическая зависимость, описывающая поведение кривой распределения вероятностей, называется дифференциальным законом распределения. Знание дифференциального закона распределения позволяет получить полную информацию о свойствах случайной величины.
Но, к сожалению, экспериментальное определение закона распределения – достаточно трудоемкая задача. Для получения относительно точной зависимости приходится производить большое количество измерений. Кроме того, необходимо иметь в виду, что найденная зависимость для определенного значения физической величины не обязательно будет в полной мере отражать закон распределения для всех остальных значений. Если требуется проверка данного факта, то трудоемкость еще увеличивается. Поэтому часто законы распределений принимаются из теоретических соображений или на основании априорных знаний. Теоретически закон распределения погрешностей результата измерения можно найти, если известны законы распределения частных погрешностей. Но практически задача усложняется тем, что законы распределения частных погрешностей не всегда известны.
Для доверительной вероятности нахождения истинного значения измеряемой величины в интервале (D1 - D2) доверительную вероятность можно записать в виде
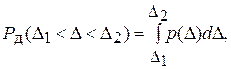(4.6)
 |
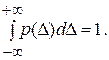где р(D) - дифференциальная плотность распределения погрешности, функция, нормированная условием
Поможем написать любую работу на аналогичную тему