Случайный характер выпадения того или иного определенного результата измерения Х означает, что причины его появления настолько разнообразны, что невозможно заранее предсказать реализацию этого события. Можно говорить только в его вероятности появления при ограниченном или бесконечно большом числе измерений. Обозначая истинное значение измеряемой величины как Q, будем под символом Xi понимать результат измерения в опыте с номером i.
Задача, которая ставится перед метрологом, желающим приблизиться к истинному значению измеряемой величины Q и оценить вероятность определенного отклонения в единичном опыте или в серии измерений, состоит в отыскании закона распределения вероятности получения определенного результата от какого-либо аргумента, связанного с отклонением результата от истинного значения. Наиболее универсальным способом достижения этой цели является отыскание интегральных и дифференциальных функций распределения вероятности.
Под интегральной функцией распределения вероятности выпадения определенного результата во множестве повторяющихся измерений (Fx ) понимается зависимость вероятности того, что результат наблюдения Х в i-ом опыте окажется меньше, чем некоторое значение х, т.е.
(3.11)
где знаком Р обозначена вероятность попадания результата в интервал, записанный в фигурных скобках.
Наглядное представление о смысле интегральной функции распределения может быть получено если рассматривать числовую ось,
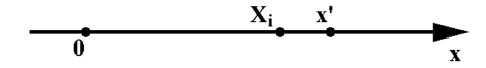
на которой отложены значения аргумента х. Интегральная функция распределения численно равна вероятности того, что случайная точка Xi , в результате i-го измерения займет положение левее точки х'.
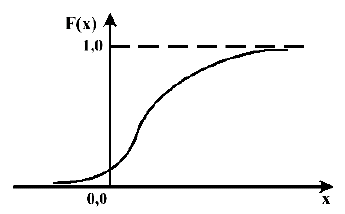
При таком определении функция распределения F(x) не может уменьшаться, т. е. F(x) является функцией возрастающей. При движении точки х' влево по числовой оси очевидно, что искомая вероятность будет стремиться к нулю, а при движении х' вправо функция F(x) стремится к единице. Это практически означает, что любой результат измерения попадет в какое-либо значение на числовой оси. Вероятность попадания в бесконечно малое значение х' равно нулю.
Интегральная функция распределения имеет еще одно свойство - непрерывность. Оно выражает тот факт, что результат наблюдения может принять любое до опыта выбранное значение только с нулевой вероятностью.
На самом деле в реальных измерениях это не совсем так. Особенно понятно это с позиций современной квантовой теории. Квантовый (дискретный) характер изменения измеряемой величины, конечная разрешающая способность любого средства измерения, приводят к тому, что область значений измеряемой величины разбивается на ряд участков, в пределах которых данная величина постоянна или неразличима для наблюдателя. Поэтому интегральная функция распределения реально изменяется скачками на некоторое значение при переходе от одного участка числовой оси к другой.
Мы будем рассматривать случай, когда ширина полос или участков постоянства функции F(x) ничтожно мала и не влияет на анализ погрешностей. Итак, интегральная функция распределения вероятности получения определенного результата при измерении является непрерывной неубывающей функцией, стремящейся к нулю при х стремящимся к минус бесконечности и к единице при х стремящимся к бесконечности
Случайную погрешность δ будем рассматривать как случайную величину, принимающую в различных опытах различные значения δi. Ее интегральную функцию будем рассматривать, поместив начало координат в точку х = Q, соответствующую истинному значению измеряемой величины, т. е.
(3.12)
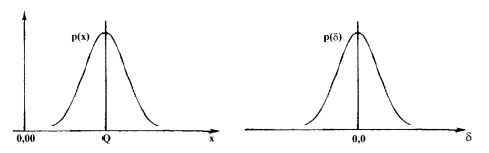
Более наглядным является описание свойств результатов наблюдений и случайных погрешностей с помощью дифференциальной функции распределения, называемой плотностью распределения вероятности. Обозначим дифференциальную функцию как Px(х) или Pδ(δ) в зависимости оттого, где расположено начало координат в изменении аргумента. Обозначение х соответствует произвольному расположению начала координат, обозначение δ соответствует помещению начала координат в точку, соответствующую истинному значению измеряемой величины (x=Q, при этом δ=0).
Дифференциальная функция распределения является производной от интегральной функции по своему аргументу
(3.13)
График дифференциальной функции распределения часто называют кривой распределения и чаще всего он имеет максимум при х = Q или при δ=0
От дифференциальной функции распределения легко перейти к интегральной путем интегрирования по интервалам: 
, т. е.
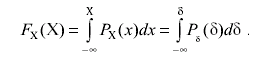(3.14)
Основным очевидным свойством дифференциальной функции распределения является равенство единице площади под кривой распределения
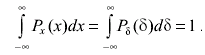(3.15)
Рассмотрим теперь физический смысл введенных понятий. Прежде всего определим вероятность попадания результата наблюдений или случайной погрешности в заданный интервал. Из определения интегральной функции распределения следует, что такая вероятность равна разности значений функции P(х) на границах интервала:
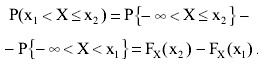(3.16)
Заменяя интегральную функцию на дифференциальную, для той же вероятности получим:
(3.17)
или
Следовательно, вероятность попадания результата измерения в заданный интервал равна площади, ограниченной кривой распределения, осью абсцисс и перпендикулярами к оси абсцисс на границах интервала. Произведения Pδ(δ)dδ и Px(x)dx называются элементами вероятности. Они равны вероятности того, что случайные величины примут значения в интервалах dδ и dx.
Следующим шагом в рассмотрении теории случайных погрешностей является определение понятия математического ожидания результата наблюдения X, т. е.:
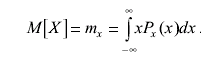(3.18)
Важное значение имеет понятие, именуемое дисперсией распределения результатов измерения D:
(3.19)
Дисперсия распределения случайной погрешности равна дисперсии результатов наблюдения и является характеристикой их рассеивания относительно математического ожидания.
Физический смысл введенных понятий становится очевидным, если переопределить с их помощью введенные нами категории систематической и случайной погрешностей.
Систематической постоянной погрешностью называется отклонение математического ожидания результатов измерения от истинного значения измеряемой величины
(3.20)
Случайной погрешностью называется разность между результатом единичного измерения и математическим ожиданием результата
(3.21)
Истинное значение, как и в предыдущих рассмотрениях, равно:
(3.22)
Если математическое ожидание рассматривать как абсциссу центра тяжести фигуры, заключенной между кривой распределения и осью Ох, то дисперсия распределения является аналогом момента инерции этой фигуры относительно вертикальной оси, проходящей через центр тяжести. Дисперсия распределения имеет размерность квадрата размерности измеряемой величины. Для удобства сопоставления в качестве определяющего параметра, характеризующего рассеяние, рассматривают арифметический корень из дисперсии, называемый средним квадратическим отклонением результатов наблюдений:
(3.23)
С помощью оценки среднего квадратического отклонения можно оценить вероятность того, что при однократном наблюдении случайная погрешность по абсолютной величине не превзойдет некоторой наперед заданной величины ε, т. е. вероятность Р = {|δ| <ε}.
Для этого запишем выражение для дисперсии распределения случайной погрешности как
(3.24)
Если сузить пределы интегрирования, то правая часть равенства возрасти не может, поэтому:
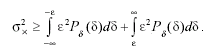(3.25)
При замене под интегралом на меньшую величину неравенство может только усилиться:
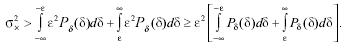(3.26)
Интегралы, стоящие в скобках, есть вероятности того, что случайная погрешность примет значения в интервалах, определяемых пределами интегрирования
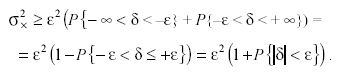(3.27)
Отсюда получаем окончательно:
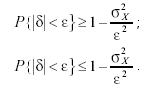(3.28)
Этот результат известен как неравенство Чебышева: вероятность того, что результат измерения выйдет за пределы произвольного интервала ±ε меньше отношения дисперсии к квадрату величины этого интервала.
Полагая ε = 3 • δx, найдем вероятность того, что результат однократного измерения выйдет за пределы утроенного среднего квадратического отклонения, т. е. вероятность того, что случайная погрешность окажется большей 3 • δx
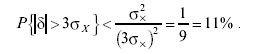(3.29)
Вероятность того, что погрешность измерения не превысит пределов Зσ соответственно составляет:
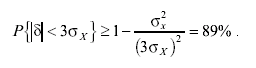(3.30)
Физический смысл неравенства ЧебышЁва состоит в том, что оно дает нижнюю границу для вероятности попадания результатов измерения в наперед заданный интервал. Меньше этого значения вероятность не может быть ни при каком распределении.
Заканчивая рассмотрение характеристик функций распределения, подведем итог, состоящий в том, что максимум математического ожидания определяет наиболее вероятное значение измеряемой величины в том случае, если разброс результатов измерений носит случайный характер. Величину этого разброса характеризует дисперсия распределения. Эти две характеристики являются наиболее употребительными, т. к. определяют наиболее близкий к истинному результат измерений и значение погрешности измерений.
В теории погрешностей иногда рассматривают так называемый третий центральный момент распределения, определяемый как
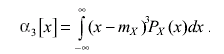(3.31)
Этот момент характеризует асимметрию или скошенность функции распределения. Чтобы получить удобную безразмерную характеристику асимметрии, вводят коэффициент асимметрии, равный отношению третьего центрального момента к кубу среднего квадратического отклонения:
(3.32)
Четвертый центральный момент, определенный как
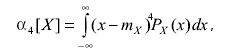(3.33)
характеризует плосковершинность или островершинность кривой распределения и выражается с помощью эксцесса - безразмерной характеристики, определяемой выражением:
(3.34)
Поможем написать любую работу на аналогичную тему