Определение доверительного интервала для выборочной дисперсии и среднеквадратического отклонения результатов измерений.
Случайная величина х имеет нормальное распределение со средним значением тх и дисперсией σх² . Оценка дисперсии выборки объема п независимых значений случайной величины х:
S² = ∑(xi – А)²/(n – 1)
Отношение k* S²/ σх² = χ²
имеет χ² (хи-квадрат) распределение Пирсона с к = п - 1 степенями свободы.
Пользуясь χ² (см. таблицу), можно найти границы доверительного интервала для оценки дисперсии результатов измерений при заданной доверительной вероятности Р = 1 - q, где q — уровень значимости.
Квантиль χ² - распределения при различных k,q
|
K |
1 – q/2 |
q/2 |
||||
|
0,99 |
0,95 |
0,90 |
0,10 |
0,05 |
0,01 Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к
профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные
корректировки и доработки. Узнайте стоимость своей работы.
|
|
|
1 2 3 4 5 6 7 8 9 10 12 14 16 18 20 30 |
0,0000157 0,0201 0,115 0,297 0,554 0,872 1,239 1,646 2,088 2,558 3,571 4,660 5,812 7.015 8,260 14,953 |
0,000393 0,103 0,352 0,711 1,145 1,635 2,167 2,733 3,325 3,940 5,226 6,571 7,962 9,390 10,851 18,493 |
0,0158 0,211 0,584 1,064 1,610 2,204 2,833 3,490 4,168 4,865 6,304 7,790 9,312 10,865 12,444 20,599 |
2,706 4,605 6,251 7,779 9,236 10,645 12,017 13,362 14,684 15,987 18,549 21,064 23,542 25,989 28,412 40,256 |
3,841 5,991 7.815 9,488 11,070 12,592 14,067 15,507 16,919 18,307 21,026 23,685 26,296 28,869 31,410 43,773 |
6,635 9,210 11,345 13,277 15,086 16,812 18,475 20,090 21,666 23,309 26,217 29,141 32,000 34,805 37,566 50,892 |
Этот интервал строится таким образом, чтобы вероятность выхода дисперсии за его границы не превышала некоторой малой величины q, причем вероятности выхода за обе границы интервала равны между собой и составляют q/2, Границы χ²| доверительного интервала находятся как
Р{ χ²k;q/2 < χ² < χ²k;1 – q/2} = 1 - q
Зная границы доверительного интервала для верительный интервал для χ² , построим доверительных интервал для дисперсии
Р{(n – 1)S²/ χ²k;q/2 < σх² < (n – 1)S²/ χ²k;1 – q/2} = 1 - q
Полученное выражение означает, что с вероятностью P = 1 - q истинное значение σх² дисперсии результатов измерений лежит в интервале (S1; S2), границы которого
S1 = (n – 1)S²/ χ²k;q/2; S2 = (n – 1)S²/ χ²k;1 – q/2
При обработке результатов измерений случайной величины, заведомо подчиняющейся нормальному закону распределения, при принятии решения об исключении или сохранении резко отклоняющихся (грубых) результатов измерений необходимо внимательно проанализировать условия, в которых получился такой результат. Сомнительным может быть лишь наибольший хмах или наименьший хмш из результатов измерений. Вопрос о том, содержит ли данный результат грубую погрешность, решается общими методами статистических гипотез. Для проверки гипотезы, что результат не содержит грубой погрешности, вычисляют
утах = (хтах - А)/S или ут!„ = (А - хт{п)/S. Результаты Ушах и Уш1п сравнивают с наибольшим значением уq, которое случайная величина V может принять по чисто случайным причинам. Значения уq для n = 3 ... 25 протабулированы и представлены в таблице при заданной доверительной вероятности или уровне значимости q.
Значения уq при различных n,q
|
n |
q |
n |
q |
||
|
0,10
|
0,05
|
0,10
|
0,05
|
||
|
3
|
1,406
|
1,412
|
15
|
2,326
|
2,493
|
|
4
|
1,645
|
1,689
|
16
|
2,354
|
2,523
|
|
5
|
1,731
|
1,869
|
17
|
2,380
|
2,551
|
|
6
|
1,894
|
1,996
|
18
|
2,404
|
2,557
|
|
7
|
1,974
|
2,093
|
19
|
2,426
|
2,600
|
|
8
|
2,041
|
2,172
|
20
|
2,447
|
2,623
|
|
9
|
2,097
|
2,237
|
21
|
2,467
|
2,644
|
|
10
|
2,146
|
2,294
|
22
|
2,486
|
2,664
|
|
11
|
2,190
|
2,383
|
23
|
2,504
|
2,683
|
|
12
|
2,229
|
2,387
|
24
|
2,520
|
2,701
|
|
13
|
2,264
|
2,426
|
25
|
2,537
|
2,717
|
|
14
|
2,297
|
2,461
|
|
|
|
Пример расчета границ доверительного интервала. Приближенно определить границы доверительного интервала, в котором с заданной вероятности Р = 0,75 находится истинное значение измеряемой величины. Известно, что sср = 0,2.
Решение. Находим по табл. П5 Прилож. аргумент t функции Ф(t) = =0,75. Значение t = 1,15. Произведение tsср = ±0,23. Следовательно, с вероятностью 0,75 истинное значение находится в интервале ±23% от измеренной величины.
Пример расчета доверительной вероятности. В результате проведения многократных наблюдений напряжения получены следующие результаты в вольтах: 19,2; 18,9; 19,4; 19,1; 18,98; 19,3. Априорно известно, что закон распределения погрешностей нормальный. Определить вероятность, с которой в интервале ± 10 % находится истинное значение измеряемого напряжения.
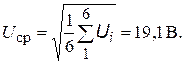Решение. За результат измерения примем
Найдем среднее квадратическое отклонение результата измерения
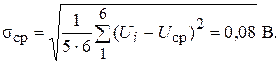
Воспользуемся формулой (6.12):
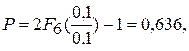
так как из табл. П6 Прилож. F(1) = 0,818 при количестве наблюдений, равном 6. Таким образом, доверительная вероятность равна 64 %.
Пример расчета границ доверительного интервала. При нормальном законе распределения погрешностей определить интервал, в котором с доверительной вероятностью 95 % находится истинное значение измеряемой физической величины. Среднее квадратическое отклонение результата измерения равно 0,05.
Решение. Преобразуем формулу (6.12) к виду
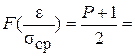
Из табл. П6 Прилож. определим значение аргумента t при значении функции 0,975 и количестве наблюдений, равном 6: t = 2,57. Отсюда e = tsср = = 2,57×0,05 = ± 0,1285.
Поможем написать любую работу на аналогичную тему