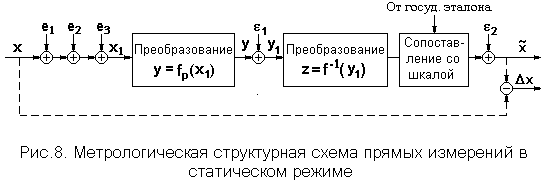
На рис. 8. приведена метрологическая структурная схема прямых измерений в статическом режиме для общего случая применения нелинейных средств измерений.
Данная схема пригодна для анализа измерений, выполняемых как аналоговыми, так и цифровыми средствами измерений, в том числе, отдельными измерительными каналами ИИС,
На рис. 8 обозначено:
x - истинное значение измеряемой величины,
![]() - погрешность, вызванная несоответствием принятой математической модели объекта и измеряемой величины их фактическим моделям (см. также пп. 2.1),
- погрешность, вызванная несоответствием принятой математической модели объекта и измеряемой величины их фактическим моделям (см. также пп. 2.1),
![]() - погрешность, вызванная взаимодействием средства измерений с объектом (см. п.2.2) ,
- погрешность, вызванная взаимодействием средства измерений с объектом (см. п.2.2) ,
![]() - погрешность, вызванная пульсациями измеряемой величины и помехами,
- погрешность, вызванная пульсациями измеряемой величины и помехами,
![]() - реальная фактическая функция преобразования конкретного экземпляра средства измерения,
- реальная фактическая функция преобразования конкретного экземпляра средства измерения,
y = f(x) - номинальная функция преобразования, декларированная для средств измерений данного типа,
![]() - функция, обратная функции y = f(x),
- функция, обратная функции y = f(x),
![]() - собственная погрешность преобразования средства измерения, вызванная дрейфом выходного сигнала преобразователя, собственными тепловыми шумами и помехами,
- собственная погрешность преобразования средства измерения, вызванная дрейфом выходного сигнала преобразователя, собственными тепловыми шумами и помехами,
![]() - погрешность, состоящая из погрешности реализации обратной функции
- погрешность, состоящая из погрешности реализации обратной функции ![]() , погрешности воспроизведения шкалы и погрешности сопоставления со шкалой, в том числе погрешности округления, выполняемого оператором при отсчете показаний аналогового прибора, или вызванного конечной разрядностью цифрового прибора или аналого-цифрового преобразователя,
, погрешности воспроизведения шкалы и погрешности сопоставления со шкалой, в том числе погрешности округления, выполняемого оператором при отсчете показаний аналогового прибора, или вызванного конечной разрядностью цифрового прибора или аналого-цифрового преобразователя,
![]() - результат прямого измерения величины x,
- результат прямого измерения величины x,
![]() - погрешность результата измерения,
- погрешность результата измерения, ![]() .
.
Различие между функциями ![]() и y = f(x) вызвано неточностью воспроизведения функции
и y = f(x) вызвано неточностью воспроизведения функции ![]() из-за погрешностей изготовления и старения комплектующих изделий, из-за воздействия внешних влияющих факторов, а также из-за разброса на множестве экземпляров средств измерений. Разность между этими функциями обозначим через
из-за погрешностей изготовления и старения комплектующих изделий, из-за воздействия внешних влияющих факторов, а также из-за разброса на множестве экземпляров средств измерений. Разность между этими функциями обозначим через ![]() . Эта разность случайна на множестве экземпляров средств измерений одного типа, и в целях обеспечения надлежащего метрологического качества должна быть ограничена пределами допускаемых различий
. Эта разность случайна на множестве экземпляров средств измерений одного типа, и в целях обеспечения надлежащего метрологического качества должна быть ограничена пределами допускаемых различий ![]() между этими функциями для всех значений измеряемой величины из диапазона измерения:
между этими функциями для всех значений измеряемой величины из диапазона измерения:
|
|
![]() .
.
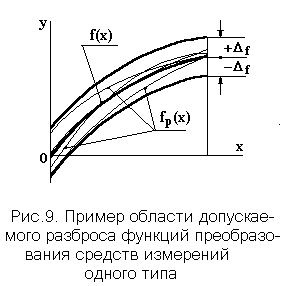
Это неравенство ограничивает область, в которой должны находиться функции преобразования всех средств измерений, признаваемых пригодными к применению. Пример такой области приведен на рис. 9.
Значение ![]() должно быть указано в технической документации на средство измерений.
должно быть указано в технической документации на средство измерений.
Естественными требованиями, предъявляемыми к функциям преобразования средств измерений, являются требования монотонности (а, следовательно, взаимной однозначности преобразования) и гладкости, то есть ограниченности модуля производных. Однако, с другой стороны, производная функции преобразования - это чувствительность средства измерений:
![]() . (1)
. (1)
Близость производных функций ![]() и y = f(x) можно выразить неравенством
и y = f(x) можно выразить неравенством
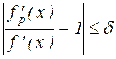
где значение d > 0 и имеет один порядок величины с собственной относительной погрешностью средства измерений.
Для удобства дальнейших рассуждений обозначим:
![]() . (2)
. (2)
Тогда, пользуясь схемой рис. 8, запишем выражение для абсолютной погрешности результата прямого измерения, выполняемого подобным средством:
![]()
и перегруппируем слагаемые:
![]() .
.
В силу монотонности функции f(x) это выражение равносильно следующему:
![]() ,
,
Применим разложение функций в степенной ряд относительно точки x и воспользовавшись малостью погрешностей, оставим только первые и линейные члены этих рядов. Тогда после перегруппировки слагаемых получим:
![]() .
.
Производная ![]() номинальной функции, то есть чувствительность средства измерений не должна быть равна нулю, поэтому мы имеем право разделить обе части последнего равенства на
номинальной функции, то есть чувствительность средства измерений не должна быть равна нулю, поэтому мы имеем право разделить обе части последнего равенства на ![]() :
:
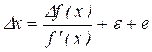 , (3)
, (3)
где 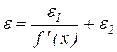 - собственная абсолютная аддитивная погрешность средства измерений.
- собственная абсолютная аддитивная погрешность средства измерений.
Первое и второе слагаемые, находящиеся в правой части равенства (3), порождены собственными свойствами средства измерений, поэтому сумма
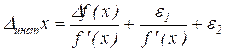 (4)
(4)
называется инструментальной составляющей абсолютной погрешности или инструментальной погрешностью. При выпуске средства измерений из производства, при его транспортировании, хранении и эксплуатации инструментальная погрешность не должна превышать (может быть, с некоторой вероятностью) некоторого заранее установленного значения ![]() . Значение
. Значение ![]() нормы погрешности
нормы погрешности ![]() , устанавливается при проектировании средства измерений и сообщается пользователю в сопроводительной технической документации. Процесс установления нормы на инструментальную погрешность называется нормированием характеристики инструментальной погрешности средства измерений. Норма погрешности
, устанавливается при проектировании средства измерений и сообщается пользователю в сопроводительной технической документации. Процесс установления нормы на инструментальную погрешность называется нормированием характеристики инструментальной погрешности средства измерений. Норма погрешности ![]() в соответствии с определением, приведенным в п. 1.5, является метрологической характеристикой средства измерений. Ответственность за инструментальную погрешность несет разработчик и производитель средства измерений.
в соответствии с определением, приведенным в п. 1.5, является метрологической характеристикой средства измерений. Ответственность за инструментальную погрешность несет разработчик и производитель средства измерений.
Последнее слагаемое в правой части равенства (3) порождено причинами, возникающими при применении средства измерений, а именно, взаимодействием с объектом, неадекватностью принятых математических моделей измеряемой величины и объекта, пульсациями и помехами, источником которых является объект. Это слагаемое составляет различие между погрешностями средства измерений и погрешностями результата измерений, и за него несут ответственность пользователи средства измерений.
Поэтому в дальнейшем будем называть погрешность ![]() погрешностью применения средства измерений. Оценку характеристики погрешности применения для конкретных условий выполняет пользователь средства измерений. Норма на эту погрешность, как правило, не устанавливается.
погрешностью применения средства измерений. Оценку характеристики погрешности применения для конкретных условий выполняет пользователь средства измерений. Норма на эту погрешность, как правило, не устанавливается.
Как было отмечено ранее в п. 1.6, значение погрешности результата каждого измерения определено быть не может, поэтому на практике пользуются оценками интервальных характеристик погрешности. Исходными данными для расчета характеристики абсолютной погрешности результата измерений в виде границ интервала неопределенности (![]() ) могут быть только предельно допускаемые значения
) могут быть только предельно допускаемые значения ![]() и
и ![]() составляющих абсолютной инструментальной погрешности, которые должны быть сообщены пользователю в технической документации на средство измерений. Гарантии в отношении сохранности этих характеристик обеспечивает изготовитель средства измерений и контролирующие метрологические органы. Предельно возможные границы (-
составляющих абсолютной инструментальной погрешности, которые должны быть сообщены пользователю в технической документации на средство измерений. Гарантии в отношении сохранности этих характеристик обеспечивает изготовитель средства измерений и контролирующие метрологические органы. Предельно возможные границы (-![]() , +
, + ![]() ) погрешности e определяются пользователем в привязке к конкретным условиям измерений.
) погрешности e определяются пользователем в привязке к конкретным условиям измерений.
Итак, если эти исходные данные известны, то есть, если известно (может быть, с некоторой вероятностью), что
![]() ,
, 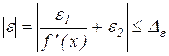 , |e| £
, |e| £ ![]() ,
,
то об абсолютной погрешности результата измерений на основании равенства (4) можно заключить, что ее значения не должны выходить за пределы, которые определяются неравенством
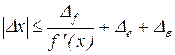 . (5)
. (5)
Таким образом границы интервала остаточной неопределенности значения измеряемой величины суть ![]() , где
, где
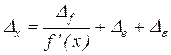 , (6)
, (6)
![]() - результат измерения.
- результат измерения.
Абсолютная инструментальная погрешность средства измерений, выраженная в единицах измеряемой величины, лежит (может быть, с некоторой вероятностью) в пределах ![]() , где
, где
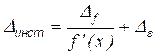 . (7)
. (7)
В рассмотренном общем случае удобно устанавливать норму ![]() на относительную инструментальную погрешность средства измерений или норму
на относительную инструментальную погрешность средства измерений или норму ![]() на погрешность, отнесенную к наибольшему значению измеряемой величины в диапазоне измерения. Такие нормы выражаются в процентах:
на погрешность, отнесенную к наибольшему значению измеряемой величины в диапазоне измерения. Такие нормы выражаются в процентах:
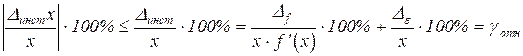 , (8)
, (8)
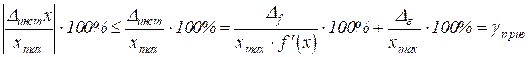 . (9)
. (9)
Поможем написать любую работу на аналогичную тему