Частная метрологическая структурная схема. Средство измерений линейное

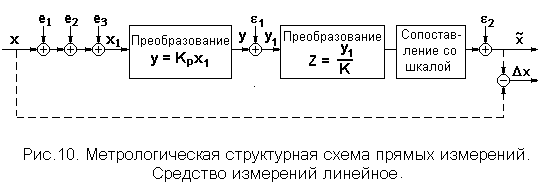
Метрологическая схема измерений в этом случае существенно упрощается (см. рис. 10).

Поскольку здесь ,  f(x) = K×x,  ,  ,

, выражение (3) для абсолютной погрешности результата измерений приобретает вид

                              ,                                             (10)

где   -  абсолютная  погрешность  коэффициента  преобразования, вызванная разбросом  его значений на множестве средств измерений данного типа, e - погрешность, возникающая при применении средства измерений,

e  - собственная абсолютная аддитивная погрешность средства измерений (инструментальная абсолютная аддитивная погрешность):

                                       .

Первое слагаемое равенства (10) линейно зависит от измеряемой величины и представляет собой произведение относительной погрешности коэффициента преобразования на значение измеряемой величины. Поэтому данная составляющая погрешности называется мультипликативной составляющей погрешности или мультипликативной погрешностью.

Второе и третье слагаемые не зависят от измеряемой величины, в сумме эти слагаемые образуют аддитивную составляющую погрешности или аддитивную погрешность результата измерений. Последнее из этих слагаемых по-

рождено собственными свойствами средства измерений, и это слагаемое является аддитивной погрешностью средства измерений. Точно так же исключительно свойствами средства измерений порождена мультипликативная составляющая погрешности (10). В связи с этим, как это было в п. 3.1.1, инструментальная составляющая абсолютной погрешности или инструментальная погрешность равна

                    (11)

По аналогии с п. 3.1.1  характеристикой разброса коэффициентов преобразования на множестве средств измерений одного типа является предельное допускаемое значение , такое, что:

           .

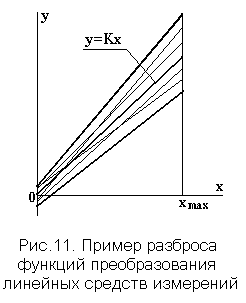
При выполнении этого условия разброс функций преобразования подобных средств измерений на множестве однотипных экземпляров будет иметь вид, показанный на рис. 11.

Как видно из рисунка, границами интервала погрешности будут расходящиеся прямые линии. В самом деле, используя обозначения  предельных  значений  составляющих  погрешности,  введенные  в  п. 3.1.1, получим линейное выражение для границ интервала , содержащего (может быть, с некоторой вероятностью) значение абсолютной погрешности результата измерений:

                                       ,                               (12)

где  - предельное значение аддитивной погрешности:

                                                        .

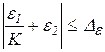Абсолютная инструментальная погрешность средства измерений лежит (может быть, с некоторой вероятностью) в пределах , где

                                        (13)

Предельное значение  относительной погрешности результата измерений выражается формулой

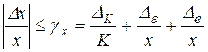,                                (14)

правая часть которой есть сумма предельно допускаемых относительных погрешностей e и e.

Здесь характеристика относительной мультипликативной составляющей уже не зависит от измеряемой величины и равна предельному значению относительной погрешности коэффициента преобразования .  Аддитивные составляющие содержат значение измеряемой величины в знаменателе, а это значит, что относительная погрешность результатов измерения увеличивается при уменьшении значений измеряемой величины.

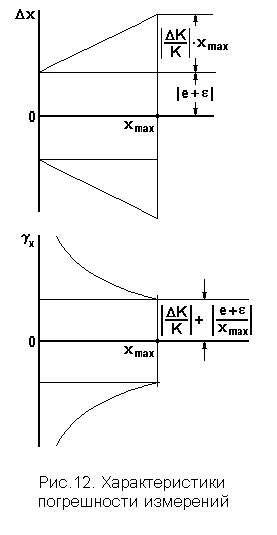
Соответствующая область возможных значений абсолютной погрешности измерений показана в верхней части рис. 12, где  - верхний предел диапазона измерения. В нижней части рис. 12 показана область возможных значений относительной погрешности.

В рассмотренном случае оказывается удобным установить раздельные нормы на две составляющие инструментальной погрешности: на относительную погрешность коэффициента преобразования и на аддитивную составляющую погрешности средства измерений. Именно так нормируется инструментальная погрешность линейных средств измерений в зарубежной практике, а именно,

- норма  устанавливается на относительную погрешность коэффициента преобразования в процентах (gain error):

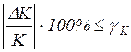                                      ,                                       (15)

- норма  устанавливается на абсолютное значение аддитивной погрешности в единицах измеряемой величины (offset error):

                                       .

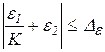В отечественной практике применяется иное нормирование инструментальной погрешности линейных средств измерений: нормируется относительная инструментальная погрешность средства измерений с помощью двучленной формулы:

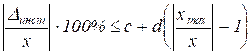                            ,                        (16)

где  - максимальное значение измеряемой величины в диапазоне измерения, x - истинное значение измеряемой величины, на практике вместо него используется результат измерения (см. также п. 1.6),

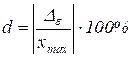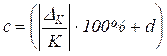                            ,          .             (17)

Раскрывая скобки в (16) с учетом обозначений (17), получим ограничение, накладываемое этой формулой на относительную инструментальную погрешность средства измерений:

                     ,

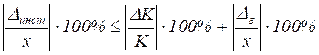что согласуется с (13). Сравнение зарубежных и отечественных методов нормирования показывает, что при отечественном нормировании пользователю предоставляется более наглядная и полная информация об инструментальной погрешности средства измерений.